Question

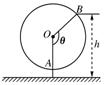
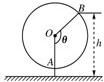如图为一个缆车示意图，该缆车半径为4.8m，圆上最低点与地面距离为0.8m，60秒转动一圈，图中OA与地面垂直，以OA为始边，逆时针转动θ角到OB，设B点与地面距离是h．
（1）求h与θ间的函数关系式；
（2）设从OA开始转动，经过t秒后到达OB，求h与t之间的函数关系式，并求缆车到达最高点时用的最少时间是多少？

Answer 1

分析：（1）以圆心O为原点，以水平方向为x轴方向，以竖直方向为Y轴方向建立平面直角坐标系，则根据缆车半径为4.8m，圆上最低点与地面距离为0.8m，60秒转动一圈，我们易得到到h与θ间的函数关系式；
（2）由60秒转动一圈，我们易得点A在圆上转动的角速度是

π

30

，故t秒转过的弧度数为

π

30

t，根据（1）的结论，我们将

π

30

t代入解析式，即可得到满足条件的t值．

解答：解：（1）以圆心O为原点，建立如图所示的平面直角坐标系，
则以Ox为始边，OB为终边的角为θ-

π

2

，
故点B的坐标为
（4.8cos(θ-

π

2

)，4.8sin(θ-

π

2

)），
∴h=5.6+4.8sin(θ-

π

2

)．
（2）点A在圆上转动的角速度是

π

30

，故t秒转过的弧度数为

π

30

t，
∴h=5.6+4.8sin(

π

30

t-

π

2

)，t∈[0，+∞）．
到达最高点时，h=10.4m．
由sin(

π

30

t-

π

2

)=1
得

π

30

t-

π

2

=

π

2

，
∴t=30
∴缆车到达最高点时，用的时间最少为30秒．

点评：本题考查的知识点是在实际问题中建立三角函数模型，在建立函数模型的过程中，以圆心O为原点，以水平方向为x轴方向，以竖直方向为Y轴方向建立平面直角坐标系，将现实问题转化为数学问题，是解答的关键．