题目内容
17．执行如图所示的程序框图，则输出的结果为（ ）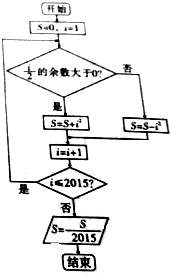
| A． | 1006 | B． | 1008 | C． | 2015 | D． | 2016 |
分析 根据程序框图进行模拟计算即可．
解答 解：当i是奇数时，$\frac{i}{2}$的余数是1＞0，S=12+…+i2，
当i是偶数时，$\frac{i}{2}$的余数0＞0不成立，S=-22-…-i2，
故程序是计算S=$\frac{1}{2015}$（12-22+32-42+…-20142+20152）
=$\frac{1}{2015}$[1+（32-22）+…+（20152-20142）]
=$\frac{1}{2015}$（1+5+9+…+4029）
=$\frac{1}{2015}$×$\frac{（1+4029）×1008}{2}$
=$\frac{1}{2015}$×$\frac{4030×1008}{2}$=1008，
故选：B
点评 本题主要考查程序框图的识别和判断，根据条件读懂程序是解决本题的关键．
练习册系列答案
相关题目
15．为了解某地高一年级男生的身高情况，从其中的一个学校选取容量为60的样本（60名男生的身高，单位：cm），分组情况如表：
则表中的a=0.45．
| 分组 | 151.5～158.5 | 158.5～165.5 | 165.5～172.5 | 172.5～179.5 |
| 频数 | 6 | 21 | 27 | 6 |
| 频率 | 0.1 | 0.35 | a | 0.1 |
12．某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在（29.94，30.06）的零件为优质品．从两个分厂生产的零件中个抽出500 件，量其内径尺寸的结果如下表（表1为甲厂，表2为乙 厂）：
表1
表2
（1）试分别估计两个分厂生产的零件的优质品率；
（2）由于以上统计数据填下面2×2列联表（填写在答题卡的2×2列联表中），并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”．
表1
| 分组 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
（2）由于以上统计数据填下面2×2列联表（填写在答题卡的2×2列联表中），并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”．
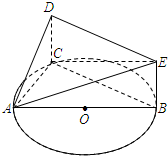如图，AB是圆O的直径，C是圆O上异于A，B的一个动点，DC垂直于圆O所在的平面，DC∥EB，DC=EB=1，AB=4．