题目内容
如图,四棱锥P-ABCD中,底面ABCD为菱形,PD=AD,∠DAB=60°,PD⊥底面ABCD.
(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3)求平面PAD与平面PBC所成锐二面角的正切值.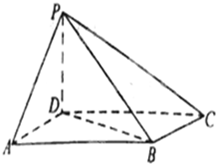
(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3)求平面PAD与平面PBC所成锐二面角的正切值.

(1)过P作BC的平行线L即为所求.(2分)

因为BC∥AD,BC?面PAD,AD⊆面PAD,
所以BC∥平面PAD,
因为平面PAD∩平面PBC=L,
所以BC∥L (5分)
(2)设PD=AD=1,设A到平面PBC的距离为h,
则由题意PA=PB=PC=
,S△ABC=
×
×
=
在等腰△PBC中,可求S△PBC=
×1×
=
∴V A-PBC=V P-ABC,
×h×
=
×1×
,h=
∴sinθ=
=
=
(3)由题意可知,PA=PB=PC=
,取BC中点M,连PM、DM,则PM⊥BC,
因为PD⊥BC,又BC∥L,
所以∠DPM为所求.(8分)
DM=DC•sin60°=
;
在Rt△PDM中,tan∠DPM=
=
=
(12分)
即平面PAD与平面PBC所成锐二面角的正切值为:
.

因为BC∥AD,BC?面PAD,AD⊆面PAD,
所以BC∥平面PAD,
因为平面PAD∩平面PBC=L,
所以BC∥L (5分)
(2)设PD=AD=1,设A到平面PBC的距离为h,
则由题意PA=PB=PC=
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
在等腰△PBC中,可求S△PBC=
| 1 |
| 2 |
(
|
| ||
| 4 |
∴V A-PBC=V P-ABC,
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 7 |
∴sinθ=
| h |
| PA |
| ||||
|
| ||
| 14 |
(3)由题意可知,PA=PB=PC=
| 2 |
因为PD⊥BC,又BC∥L,
所以∠DPM为所求.(8分)
DM=DC•sin60°=
| ||
| 2 |
在Rt△PDM中,tan∠DPM=
| DM |
| PD |
| ||||
| 1 |
| ||
| 2 |
即平面PAD与平面PBC所成锐二面角的正切值为:
| ||
| 2 |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=