题目内容
已知在数列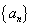 中,
中,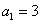 ,
, ,
,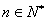 .
.
(1)证明数列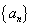 是等差数列,并求
是等差数列,并求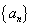 的通项公式;
的通项公式;
(2)设数列 的前
的前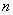 项和为
项和为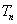 ,证明:
,证明: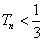 .
.
解:(1)方法一:
由 ,得
,得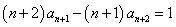 , (2分)
, (2分)
两式相减,得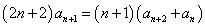 ,即
,即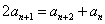 , (4分)
, (4分)
所以数列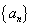 是等差数列. (5分)
是等差数列. (5分)
由 ,得
,得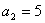 ,所以
,所以 , (6分)
, (6分)
故
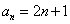 . (8分)
. (8分)
方法二:
将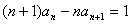 两边同除以
两边同除以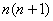 ,得
,得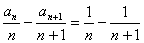 ,(3分)
,(3分)
即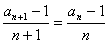 . (4分)
. (4分)
所以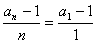 (5分)
(5分)
所以 (6分)
(6分)
因为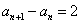 ,所以数列
,所以数列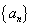 是等差数列. (8分)
是等差数列. (8分)
(2)因为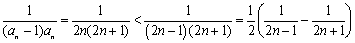 , (11分)
, (11分)
所以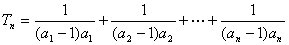
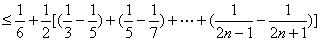
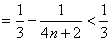 (
(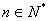 ) (14分)
) (14分)

练习册系列答案
相关题目
 表示的平面区域为D,若函数
表示的平面区域为D,若函数 的图像上存在区域D上的点,则实数
的图像上存在区域D上的点,则实数 的取值范围是( )
的取值范围是( ) (B)
(B)
 (D)
(D)
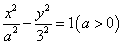 的离心率为2,则
的离心率为2,则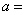 ________.
________.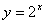 图象上存在点(x,y)满足约束条件
图象上存在点(x,y)满足约束条件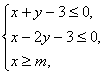 则实数m的最大值为
则实数m的最大值为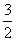 C.1 D.
C.1 D.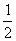
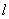 的方程为
的方程为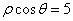 ,则点
,则点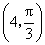 到直线
到直线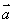 、
、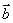 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使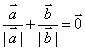 成立的是
成立的是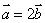 B.
B. C.
C.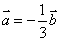 D.
D.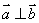
 值的一个程序框图,其中判断框内应填入的条件是
值的一个程序框图,其中判断框内应填入的条件是
 B.
B. C.
C. D.
D.
 的值是
的值是 A.
A. B.
B. C.
C. D.
D.
