题目内容
如图，PAB、PC分别是圆O的割线和切线（C为切点），若PA=AB=3，则PC的长为
- A.
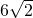
- B.6
- C.
- D.3
C
分析：由题意可得：设圆的圆心为O，半径为r，所以OC=OA=r．由圆的性质可得：PC2=OP2-r2，OD2+1.52=r2，OD2+4.52=OP2，进而得到答案．
解答：由题意可得：设圆的圆心为O，半径为r，所以OC=OA=r．
由圆的性质可得：PC2=OP2-r2，
又因为PA=AB=3，所以AD=1.5．
所以OD2+1.52=r2…①
OD2+4.52=OP2…②
所以②-①可得：OP2-r2=4.52-1.52=18，
所以PC=．
故选C．
点评：解决此类问题的关键是熟练掌握圆与直线的位置关系，以及圆的有关性质即构成的直角三角形．
分析：由题意可得：设圆的圆心为O，半径为r，所以OC=OA=r．由圆的性质可得：PC2=OP2-r2，OD2+1.52=r2，OD2+4.52=OP2，进而得到答案．
解答：由题意可得：设圆的圆心为O，半径为r，所以OC=OA=r．
由圆的性质可得：PC2=OP2-r2，
又因为PA=AB=3，所以AD=1.5．
所以OD2+1.52=r2…①
OD2+4.52=OP2…②
所以②-①可得：OP2-r2=4.52-1.52=18，
所以PC=
．故选C．
点评：解决此类问题的关键是熟练掌握圆与直线的位置关系，以及圆的有关性质即构成的直角三角形．
练习册系列答案
相关题目
如图，PAB、PC分别是圆O的割线和切线（C为切点），若PA=AB=3，则PC的长为（ ）A、6
| ||
| B、6 | ||
C、3
| ||
| D、3 |
如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点E、D分别是AC、PC的中点，EP⊥底面ABC．
如图，已知四棱锥P-ABCD中，侧棱PA⊥平面ABCD，底面ABCD是平行四边形，PB=PC，AB=1，
