题目内容
已知椭圆 :
: (
( )的离心率
)的离心率 ,直线
,直线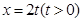 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当圆 与
与 轴相切的时候,求
轴相切的时候,求 的值;
的值;
(Ⅲ)若 为坐标原点,求
为坐标原点,求 面积的最大值。
面积的最大值。
(Ⅰ)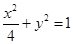 ;(Ⅱ)
;(Ⅱ)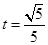 ;(Ⅲ)1.
;(Ⅲ)1.
解析试题分析:(Ⅰ)∵椭圆 的离心率
的离心率
∴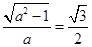 ............................1分
............................1分
解得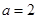 ............................2分
............................2分
故椭圆 的方程为
的方程为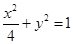 .................3分
.................3分
(Ⅱ)联立方程可得: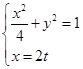 得
得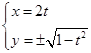 .........................5分
.........................5分
即 的坐标分别为
的坐标分别为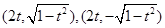 ........................6分
........................6分
∵圆 的直径为
的直径为 ,且与
,且与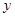 轴相切
轴相切
∴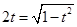 ,得
,得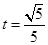 (∵
(∵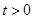 )............8分
)............8分
(Ⅲ)由(Ⅱ)可得, 的面积
的面积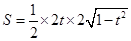 ......................9分
......................9分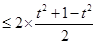
=1...................10分
当且仅当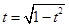 即
即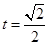 时,等号成立.....................11分
时,等号成立.....................11分
故 的面积的最大值为1..................12分
的面积的最大值为1..................12分
考点:椭圆的简单性质;圆的简单性质;直线与椭圆的综合应用;基本不等式。
点评:充分理解圆C与y轴相切的含义是做本题的关键。要满足圆C与y轴相切也就是满足M点的纵坐标与横坐标相等。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
 .
. :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B. 的中心为
的中心为 ,长轴的两个端点为
,长轴的两个端点为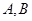 ,右焦点为
,右焦点为 ,
, .若椭圆
.若椭圆 ,
, 上的射影为
上的射影为 的面积为5.
的面积为5. =1,直线
=1,直线 =1,试证明:当点
=1,试证明:当点 在椭圆
在椭圆 与圆
与圆
 过点
过点 .
. 轴上的圆
轴上的圆 过点
过点 的切线恰是抛物线在点
的切线恰是抛物线在点 为
为 是点
是点 关于原点的对称点,过点
关于原点的对称点,过点 两点,若
两点,若 ,证明:
,证明: .
.
 ,一个焦点是F(0,1).
,一个焦点是F(0,1). 过点F交椭圆于A、B两点,且
过点F交椭圆于A、B两点,且 ,求直线
,求直线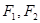 分别是椭圆
分别是椭圆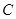 :
: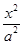 +
+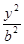 =1(
=1(
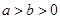 )的左、右焦点,
)的左、右焦点,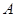 是椭圆
是椭圆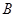 是直线
是直线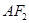 与椭圆
与椭圆
 =60°.
=60°.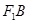 的面积为40
的面积为40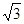 ,求a, b 的值.
,求a, b 的值.  ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状.
的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状.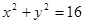 上的一个动点,过点P作PD垂直于
上的一个动点,过点P作PD垂直于 轴,垂足为D,Q为线段PD的中点。
轴,垂足为D,Q为线段PD的中点。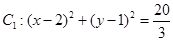 ,椭圆
,椭圆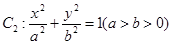 ,若
,若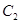 的离心率为
的离心率为 ,如果
,如果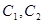 相交于
相交于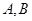 两点,且线段
两点,且线段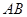 恰为圆
恰为圆 的直径,求直线
的直径,求直线