题目内容

已知二次函数f（x）=x2+2bx+c（b，c∈R）．
（1）若f（x）≤0的解集为{x|-1≤x≤1}，求实数b，c的值；
（2）若f（x）满足f（1）=0，且关于x的方程f（x）+x+b=0的两个实根分别在区间（-3，-2）和（0，1）内，求实数b的取值范围．

精英家教网
（1）因为f（x）≤0的解集为{x|-1≤x≤1}，
所以x2+2bx+c=0的根为-1，1．
故-1+1=-2b?b=0；
（-1）×1=c?c=-1．
所以b=0，c=-1．
（2）因为f（1）=0，所以1+2b+c=0?c=-2b-1．
所以f（x）+x+b=0即为x2+（2b+1）x-b-1=0．
令g（x）=x2+（2b+1）x-b-1
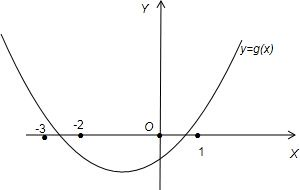
∵g（x）=f（x）+x+b=0的两个实根分别在区间（-3，-2）和（0，1）内，如图示
∴
g(0)＜0
g(1)＞0
g(-3)＞0
g(-2)＜0
?
b＞-1
b＞-1
b＞
1
5
b＜
5
7
?
1
5
＜b＜
5
7

故实数b的取值范围是
1
5
＜b＜
5
7
．
练习册系列答案
相关题目
已知二次函数f（x）=x2+2（m-2）x+m-m2．
（I）若函数的图象经过原点，且满足f（2）=0，求实数m的值．
（Ⅱ）若函数在区间[2，+∞）上为增函数，求m的取值范围．
已知二次函数f（x）=ax2+bx+c（a≠0）的图象过点（0，1），且与x轴有唯一的交点（-1，0）．
（Ⅰ）求f（x）的表达式；
（Ⅱ）设函数F（x）=f（x）-kx，x∈[-2，2]，记此函数的最小值为g（k），求g（k）的解析式．
已知二次函数f（x）=x2-16x+q+3．
（1）若函数在区间[-1，1]上存在零点，求实数q的取值范围；
（2）若记区间[a，b]的长度为b-a．问：是否存在常数t（t≥0），当x∈[t，10]时，f（x）的值域为区间D，且D的长度为12-t？请对你所得的结论给出证明．
（2013•广州一模）已知二次函数f（x）=x2+ax+m+1，关于x的不等式f（x）＜（2m-1）x+1-m2的解集为（m，m+1），其中m为非零常数．设g(x)=
f(x)x-1
．
（1）求a的值；
（2）k（k∈R）如何取值时，函数φ（x）=g（x）-kln（x-1）存在极值点，并求出极值点；
（3）若m=1，且x＞0，求证：[g（x+1）]n-g（xn+1）≥2n-2（n∈N*）．
（1）已知二次函数f（x）的图象与x轴的两交点为（2，0），（5，0），且f（0）=10，求f（x）的解析式．
（2）已知二次函数f（x）的图象的顶点是（-1，2），且经过原点，求f（x）的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网