Question

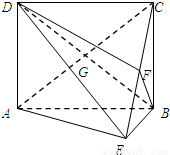
如图，矩形ABCD中，AD⊥平面ABE，AE=EB=BC，F为CE上的点，且BF⊥平面ACE．
（1）求证：AE⊥平面BCE；
（2）求证：AE∥平面BFD．

Answer 1

【答案】分析：（1）根据AD⊥平面ABE，AD∥BC可得BC⊥平面ABE，根据线面垂直的性质可知AE⊥BC，根据BF⊥平面ACE，则AE⊥BF，而BC∩BF=B，满足线面垂直的判定定理，从而证得结论；
（2）依题意可知G是AC中点，根据BF⊥平面ACE，则CE⊥BF，而BC=BE，从而F是EC中点，根据中位线定理可知FG∥AE
又FG?平面BFD，AE?平面BFD，满足线面平行的判定定理的三个条件，从而得证．
解答：解：（1）证明：∵AD⊥平面ABE，AD∥BC
∴BC⊥平面ABE，而AE?平面ABE则AE⊥BC（2分）
又∵BF⊥平面ACE，而AE?面ACE，则AE⊥BF，BC∩BF=B
∴AE⊥平面BCE（5分）
（2）证明：依题意可知：G是AC中点（6分）
∵BF⊥平面ACE，则CE⊥BF，
而BC=BE
∴F是EC中点（9分）
在△AEC中，FG∥AE
又FG?平面BFD，AE?平面BFD
∴AE∥平面BFD（12分）
点评：本题主要考查了线面垂直的判定，以及线面平行的判定和线面垂直的性质，同时考查了推理论证的能力，属于中档题．