题目内容
 的内角A、B、C的对边分别是a、b、c,且a2-c2 +b2<0 ,则角C是 ( )
的内角A、B、C的对边分别是a、b、c,且a2-c2 +b2<0 ,则角C是 ( )
A.小于600的角 B. 钝角 C.锐角 D. 都有可能
B
解析试题分析:根据题意,由于 的内角A、B、C的对边分别是a、b、c,且a2-c2 +b2<0,则根据余弦定理可知
的内角A、B、C的对边分别是a、b、c,且a2-c2 +b2<0,则根据余弦定理可知 ,故可知角C为钝角,故选B.
,故可知角C为钝角,故选B.
考点:余弦定理
点评:本题考查余弦定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用余弦定理加以判断即可

练习册系列答案
相关题目
已知 中,AB=AC=5,BC=6,则
中,AB=AC=5,BC=6,则 的面积为
的面积为
| A.12 | B.15 | C.20 | D.25 |
在 中,
中, ,则
,则 等于( )
等于( )
A. | B. | C. | D.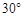 |
在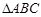 中,角
中,角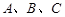 的对边长分别为
的对边长分别为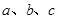 ,若
,若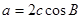 ,则
,则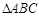 的形状为
的形状为
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.等腰直角三角形 |
在 中,角
中,角 所对的边分
所对的边分 .若
.若 ,
,
A.- | B. | C.-1 | D.1 |
在△ABC中,若b=2 ,a=2,且三角形有解,则A的取值范围是( )
,a=2,且三角形有解,则A的取值范围是( )
| A.0°<A<30° | B.0°<A≤45° | C.0°<A<90° | D.30°<A<60° |
已知△ABC中,a=4,b=4 ,∠A=30°,则∠B等于( )
,∠A=30°,则∠B等于( )
| A.30° | B.30°或150° | C.60° | D.60°或120° |
某人要制作一个三角形,要求它的三条高的长度分别为 ,则此人能( )
,则此人能( )
| A.不能作出这样的三角形 | B.作出一个锐角三角形 |
| C.作出一个直角三角形 | D.作出一个钝角三角形 |
 两地相距
两地相距 ,且
,且 地在
地在 地的正东方。一人在
地的正东方。一人在 在正北方,建筑
在正北方,建筑 在北偏西
在北偏西 ;在
;在 ,建筑
,建筑 ,则两建筑
,则两建筑



