题目内容
A．（不等式选讲） 不等式|x-1|+|x+3|＞a，对一切实数x都成立，则实数a的取值范围为______．
B．（几何证明选讲）如图，P是圆O外一点，过P引圆O的两条割线PAB、PCD，PA=AB=
，CD=3，则PC=______．
C．（极坐标系与参数方程）极坐标方程ρsin2θ-2•cosθ=0表示的直角坐标方程是______．
B．（几何证明选讲）如图，P是圆O外一点，过P引圆O的两条割线PAB、PCD，PA=AB=
| 5 |
C．（极坐标系与参数方程）极坐标方程ρsin2θ-2•cosθ=0表示的直角坐标方程是______．
A．不等式|x-1|+|x+3|＞a恒成立时，a小于左边的最小值
∵|x-1|+|x+3|≥|（x-1）-（x+3）|=4，
∴a＜4，得实数a的取值范围为（-∞，4）
B．∵PAB、PCD是圆O的两条割线，
∴PA•PB=PC•PD，得PA（PA+AB）=PC（PC+CD）
代入题中数据，得
（
+
）=PC（PC+3），解之得PC=2（舍-5）
C．极坐标方程ρsin2θ-2•cosθ=0两边都乘以ρ，得ρ2sin2θ-2•ρcosθ=0
∵ρsinθ=y，ρcosθ=x
∴原极坐标方程可化为：y2-2x=0，即y2=2x
故答案为：（-∞，4），2，y2=2x
∵|x-1|+|x+3|≥|（x-1）-（x+3）|=4，
∴a＜4，得实数a的取值范围为（-∞，4）
B．∵PAB、PCD是圆O的两条割线，
∴PA•PB=PC•PD，得PA（PA+AB）=PC（PC+CD）
代入题中数据，得
| 5 |
| 5 |
| 5 |
C．极坐标方程ρsin2θ-2•cosθ=0两边都乘以ρ，得ρ2sin2θ-2•ρcosθ=0
∵ρsinθ=y，ρcosθ=x
∴原极坐标方程可化为：y2-2x=0，即y2=2x
故答案为：（-∞，4），2，y2=2x
练习册系列答案
相关题目
（A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是
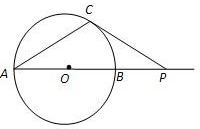A．（不等式选讲选做题）若不等式|x+1|+|x-2|＜a无实数解，则a的取值范围是
A．（不等式选讲选做题）如果存在实数x使不等式|x+1|-|x-2|＜k成立，则实数k的取值范围是
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）