题目内容
已知函数y=2sin2
-cos 2x，则它的周期T和图象的一条对称轴方程是（ ）A．T=2π，x=
B．T=2π，x=
C．T=π，x=
D．T=π，x=
【答案】分析：先利用二倍角公式和两角和公式对函数解析式进行化简，进而根据正弦函数的性质可求得函数的周期和对称轴，求得答案．
解答：解：∵y=2sin2
-cos2x=1-cos
-cos2x=1+sin2x-cos2x=1+
sin
，
所以其周期T=π，对称轴方程的表达式可由2x-
=kπ+
（k∈Z）得x=
+
（k∈Z），
故当k=0时的一条对称轴方程为x=
．
故选D．
点评：本题主要考查了两角和公式，二倍角公式，正弦函数的周期性和对称性等问题．解题的关键是对三角函数基础知识的全面掌握．
解答：解：∵y=2sin2
-cos2x=1-cos-cos2x=1+sin2x-cos2x=1+sin，所以其周期T=π，对称轴方程的表达式可由2x-
=kπ+（k∈Z）得x=+（k∈Z），故当k=0时的一条对称轴方程为x=
．故选D．
点评：本题主要考查了两角和公式，二倍角公式，正弦函数的周期性和对称性等问题．解题的关键是对三角函数基础知识的全面掌握．
练习册系列答案
教材全解字词句篇系列答案
相关题目
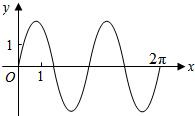已知函数y=2sin（ωx+φ）（ω＞0））在区间[0，2π]的图象如图：那么ω=（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin（wx+θ）为偶函数，其图象与直线y=2某两个交点的横坐标分别为x1，x2，若|x2-x1|的最小值为π，则该函数在区间（ ）上是增函数．
A、(-
| ||||
B、(-
| ||||
C、(0，
| ||||
D、(
|
下列4个命题：