题目内容
已知下列命题:
①设m为直线, 为平面,且m
为平面,且m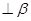 ,则“m//
,则“m// ”是“
”是“ ”的充要条件;
”的充要条件;
② 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则P(-2<
≥2)=p,则P(-2< <0)=
<0)= ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是( ,2);
,2);
⑤已知奇函数 满足
满足 ,且0<x<
,且0<x<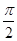 时
时 ,则函数
,则函数 在[
在[ ,
, ]上有5个零点.
]上有5个零点.
其中真命题的序号是 (写出全部真命题的序号).
③
解析试题分析:解:①因为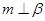 ,所以,由
,所以,由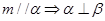 成立,
成立,
但由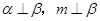 ,可得到
,可得到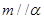 或
或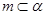 ,所以
,所以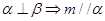 不成立,故该命题为假命題;
不成立,故该命题为假命題;
② 的展开式中第
的展开式中第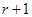 项
项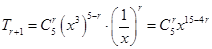 ,
,
令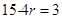 ,解得
,解得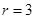 ,所以有
,所以有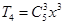 =
=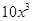 ,
, 的展开式中含x3的项的系数为10而不是60;故该命题是假命题.
的展开式中含x3的项的系数为10而不是60;故该命题是假命题.
③由随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则
≥2)=p,则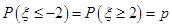 ,
,
所以,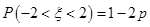
所以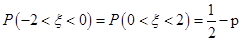 ;该命题是真命题;
;该命题是真命题;
④因为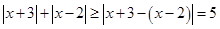
所以有,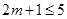 ,解得
,解得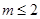
由此可知④是假命.
⑤因为奇函数 满足
满足 ,所以,
,所以,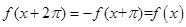 ,故函数
,故函数 是周期函数,且
是周期函数,且 ;同样由奇函数
;同样由奇函数 满足
满足 ,
,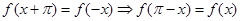
所以函数 的图象关于直线
的图象关于直线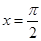 对称;
对称;
因为奇函数 满足当0<x<
满足当0<x<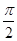 时
时 得当
得当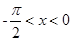 时,
时,  ,
,
又因为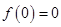
由以上条件在同一坐标系中画出函数 和
和 的图象如下图,则两图象在区间
的图象如下图,则两图象在区间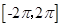 内交点的个数就是函数
内交点的个数就是函数 在区间
在区间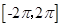 内的零点的个数;但由于
内的零点的个数;但由于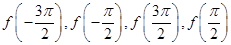 的值不能确定,故零点的个数不能确定,
的值不能确定,故零点的个数不能确定,
所以该命题是假命题.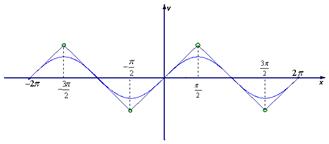
所以答案应填③
考点:1、命题;2、直线与平面的位置关系;3、二项式定理;4、正态密度曲线的性质;5、函数的性质与函数的零点.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目





 ,
, 是空间中两条不同的直线,
是空间中两条不同的直线, ,
, ,
, 是空间中三个不同的平面,则
是空间中三个不同的平面,则 下列命题正确的序号是 .
下列命题正确的序号是 . ,
, ,则
,则 ; ②若
; ②若 ,则
,则 ;
; ,
, ; ④若
; ④若 ,则
,则 β;②a∥γ,b∥β;③b∥β,a
β;②a∥γ,b∥β;③b∥β,a γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).
γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).