Question

如图所示，直三棱柱ABC—A₁B₁C₁中，B₁C₁=A₁C₁，AC₁⊥A₁B，M、N分别是A₁B₁、AB的中点.

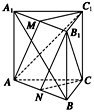
（1）求证：C₁M⊥平面A₁ABB₁；

（2）求证：A₁B⊥AM；

（3）求证：平面AMC₁∥平面NB₁C；

（4）求A₁B与B₁C所成的角.

Answer 1

证明略，（4）A₁B与B₁C所成的角为90°

解析:

（1）  方法一  由直棱柱性质可得AA₁⊥平面A₁B₁C₁，

又∵C₁M平面A₁B₁C₁，∴AA₁⊥MC₁.

又∵C₁A₁=C₁B₁，M为A₁B₁中点，∴C₁M⊥A₁B₁.

又A₁B₁∩A₁A=A₁，∴C₁M⊥平面AA₁B₁B.

方法二   由直棱柱性质得：平面AA₁B₁B⊥平面A₁B₁C₁，交线为A₁B₁，又∵C₁A₁=C₁B₁，M为A₁B₁的中点，

∴C₁M⊥A₁B₁于M.

由面面垂直的性质定理可得C₁M⊥平面AA₁B₁B.

（2）  由（1）知C₁M⊥平面A₁ABB₁，

∴C₁A在侧面AA₁B₁B上的射影为MA.

∵AC₁⊥A₁B，MC₁⊥A₁B，MC₁∩AC₁=C₁，

∴A₁B⊥平面AMC₁，又AM平面AMC₁，∴A₁B⊥AM.

（3）方法一   由棱柱性质知四边形AA₁B₁B是矩形，

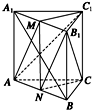M、N分别是A₁B₁、AB的中点，

∴ANB₁M.

∴四边形AMB₁N是平行四边形.

∴AM∥B₁N.

连接MN，在矩形AA₁B₁B中有

A₁B₁AB.

∴MB₁ BN，∴四边形BB₁MN是平行四边形.

∴BB₁  MN.又由BB₁ CC₁，知MN CC₁.

∴四边形MNCC₁是平行四边形.∴C₁MCN.

又C₁M∩AM=M，CN∩NB₁=N，

∴平面AMC₁∥平面NB₁C.

方法二  由（1）知C₁M⊥平面AA₁B₁B，

A₁B平面AA₁B₁B，∴C₁M⊥A₁B.

又∵A₁B⊥AC₁，而AC₁∩C₁M=C₁，

∴A₁B⊥平面AMC₁.

同理可证，A₁B⊥平面B₁NC.

∴平面AMC₁∥平面B₁NC.

(4)  方法一  由（2）知A₁B⊥AM，

又由已知A₁B⊥AC₁，AM∩AC₁=A，

∴A₁B⊥平面AMC₁.

又∵平面AMC₁∥平面NB₁C，

∴A₁B⊥平面NB₁C.

又B₁C平面NB₁C，∴A₁B⊥B₁C.

∴A₁B与B₁C所成的角为90°.

方法二  由直棱柱的性质有平面ABC⊥平面AA₁B₁B，交线为AB，又CA=CB=C₁A₁，N为AB的中点，

∴CN⊥AB.

∴CN⊥平面AA₁B₁B.

∴CB₁在侧面AA₁B₁B上的射影是NB₁.

又由（2）知A₁B⊥AM，由（3）知B₁N∥AM，

∴A₁B⊥B₁N，CN⊥A₁B，

∴A₁B⊥平面B₁NC，又B₁C平面B₁NC，∴A₁B⊥B₁C.

∴A₁B与B₁C所成的角为90°.