题目内容
已知n是正整数,在数列{an}中,a1=1,an+1=2an+1,在数列{bn}中,b1=a1,
当n≥2时, =
= +
+ +…+
+…+ .
.
(I)求数列{an}的通项公式:
(II)求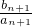 -
- 的值:
的值:
(III)当n≥2时,证明:
 .
.
解:(I)∵an+1=2an+1,
两边同加1得,an+1+1=2(an+1),
∴数列{an+1+1}是以a1+1=2为首项,以2为公比的等比数列.
∴an+1=2×2n-1=2n,
∴an=2n-1
(II)∵ ,b1-a1=1
,b1-a1=1
∴ =-1
=-1
∴当n=1时,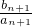
 =-1
=-1
当n≥2时,
∵ =
=
∴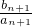 =
=
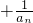 =
= =
=
∴ =0
=0
综上所述,当n=1时 =-1
=-1
当n≥2时 =0.
=0.
(III)由(II)知:b1=a1=1, ,即b2=a2=3.
,即b2=a2=3.
当n≥2时, =0,即
=0,即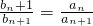
∴当n≥2时,
=
=
= =2×
=2×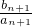
=2×( )
)
=2×(1+ )
)
>2(1+ )
)
=2[1+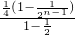 ]=3-
]=3-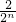 .
.
∴当n≥2时,
 .
.
分析:(I)将an+1=2an+1两端同加上1,整理,构造出等差或等比数列,进行解决.
(II)根据已知写出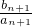 的表达式,再考虑作差.注意对n=1的讨论.
的表达式,再考虑作差.注意对n=1的讨论.
(III)将 变形为
变形为 ,除首尾两项外,中间项根据(Ⅱ)的结果,进行代换,同时要注意放缩法在过程中适时、适当的适用.
,除首尾两项外,中间项根据(Ⅱ)的结果,进行代换,同时要注意放缩法在过程中适时、适当的适用.
点评:本题考查等比数列的定义,通过对递推式变形,构造出特殊的数列来解决问题的能力,计算能力,以及分析问题解决问题的能力.(I)的两边加一个合适的常数的方法适用于形如:已知an+1=pan+q(pq≠0),求an.(III)虽 的分子分母具有明显的对应特征,但若把目光放在对
的分子分母具有明显的对应特征,但若把目光放在对 (k=1,2,…,n)的处理上,则使问题脱离已经挖掘出的新信息(Ⅱ),走向偏离.因此本题同时要求获取信息,灵活综合分析解决问题的能力.
(k=1,2,…,n)的处理上,则使问题脱离已经挖掘出的新信息(Ⅱ),走向偏离.因此本题同时要求获取信息,灵活综合分析解决问题的能力.
两边同加1得,an+1+1=2(an+1),
∴数列{an+1+1}是以a1+1=2为首项,以2为公比的等比数列.
∴an+1=2×2n-1=2n,
∴an=2n-1
(II)∵
 ,b1-a1=1
,b1-a1=1∴
 =-1
=-1∴当n=1时,
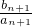
 =-1
=-1当n≥2时,
∵
 =
=
∴
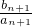 =
=
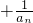 =
= =
=
∴
 =0
=0综上所述,当n=1时
 =-1
=-1当n≥2时
 =0.
=0.(III)由(II)知:b1=a1=1,
 ,即b2=a2=3.
,即b2=a2=3.当n≥2时,
 =0,即
=0,即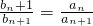
∴当n≥2时,

=

=

=
 =2×
=2×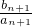
=2×(
 )
)=2×(1+
 )
)>2(1+
 )
)=2[1+
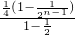 ]=3-
]=3-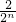 .
.∴当n≥2时,

 .
.分析:(I)将an+1=2an+1两端同加上1,整理,构造出等差或等比数列,进行解决.
(II)根据已知写出
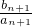 的表达式,再考虑作差.注意对n=1的讨论.
的表达式,再考虑作差.注意对n=1的讨论.(III)将
 变形为
变形为 ,除首尾两项外,中间项根据(Ⅱ)的结果,进行代换,同时要注意放缩法在过程中适时、适当的适用.
,除首尾两项外,中间项根据(Ⅱ)的结果,进行代换,同时要注意放缩法在过程中适时、适当的适用.点评:本题考查等比数列的定义,通过对递推式变形,构造出特殊的数列来解决问题的能力,计算能力,以及分析问题解决问题的能力.(I)的两边加一个合适的常数的方法适用于形如:已知an+1=pan+q(pq≠0),求an.(III)虽
 的分子分母具有明显的对应特征,但若把目光放在对
的分子分母具有明显的对应特征,但若把目光放在对 (k=1,2,…,n)的处理上,则使问题脱离已经挖掘出的新信息(Ⅱ),走向偏离.因此本题同时要求获取信息,灵活综合分析解决问题的能力.
(k=1,2,…,n)的处理上,则使问题脱离已经挖掘出的新信息(Ⅱ),走向偏离.因此本题同时要求获取信息,灵活综合分析解决问题的能力. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

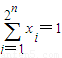 ,证明:
,证明: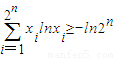
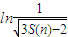 (i,n∈N*).
(i,n∈N*).