Question

（本小题满分12分）

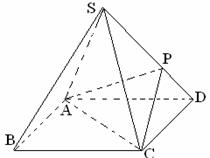
如图，四棱锥S-ABCD 的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点．

(Ⅰ) 求证：AC⊥SD；

(Ⅱ) 若SD⊥平面PAC，求二面角                                P-AC-D的大小

(Ⅲ) 在（Ⅱ）的条件下，侧棱SC上是                                  否存在一点E，使得BE∥平面PAC？若存在，求SE：EC的值；若不存在，试说明理由．

Answer 1

【解法一】：（Ⅰ）连BD，设AC交BD于O，由题意。在正方形ABCD中，，所以,得.  ……………（4分）

(Ⅱ)设正方形边长，则。又，所以,

连，由（Ⅰ）知,所以,

且,所以是二面角的平面角。

由,知,所以,

即二面角的大小为。  ……………………………（8分）

（Ⅲ）在棱SC上存在一点E，使

由（Ⅱ）可得，故可在上取一点,使,过作的平行线与的交点即为。连BN。在中知，又由于,故平面，得,由于,故.

   ……………………………………………………………………（12分）

【解法二】：（Ⅰ）；连,设交于于，由题意知.以O为坐标原点，分别为轴、轴、轴正方向，建立坐标系

设底面边长为，则高。

于是，，

，，故 ，从而

(Ⅱ)由题设知，平面的一个法向量，平面的一个法向量，设所求二面角为，则,所求二面角的大小为

（Ⅲ）在棱上存在一点使.

由（Ⅱ）知是平面的一个法向量，

且

设则

而，即当时，_，

而不在平面内，故