题目内容
已知m,n,s,t∈R+,m+n=2,
+
=9,其中m、n是常数,当s+t取最小
时,m、n对应的点(m,n)是双曲线
-
=1一条弦的中点,则此弦所在的直线方程为( )
| m |
| s |
| n |
| t |
| 4 |
| 9 |
| x2 |
| 4 |
| y2 |
| 2 |
| A.x-2y+1=0 | B.2x-y-1=0 | C.2x+y-3=0 | D.x+2y-3=0 |
由已知得s+t=
(s+t)(
+
)=
(m+n+
+
)≥
(m+n+2
)=
(
+
)2,
由于s+t的最小值是
,
因此
(
+
)2=
,即
+
=2,又m+n=2,
所以m=n=1.
设以点(m,n)为中点的弦的两个端点的坐标分别是(x1,y1),(x2,y2),
则有
=
=1,即x1+x2=y1+y2=2①.
又该两点在双曲线上,则有
-
=1,
-
=1,
两式相减得
-
=0②,
把①代入②得
=
,
即所求直线的斜率是
,所求直线的方程是y-1=
(x-1),即x-2y+1=0.
故选A
| 1 |
| 9 |
| m |
| s |
| n |
| t |
| 1 |
| 9 |
| mt |
| s |
| ns |
| t |
| 1 |
| 9 |
| mn |
| 1 |
| 9 |
| m |
| n |
由于s+t的最小值是
| 4 |
| 9 |
因此
| 1 |
| 9 |
| m |
| n |
| 4 |
| 9 |
| m |
| n |
所以m=n=1.
设以点(m,n)为中点的弦的两个端点的坐标分别是(x1,y1),(x2,y2),
则有
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
又该两点在双曲线上,则有
| x12 |
| 4 |
| y12 |
| 2 |
| x22 |
| 4 |
| y22 |
| 2 |
两式相减得
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 4 |
把①代入②得
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
即所求直线的斜率是
| 1 |
| 2 |
| 1 |
| 2 |
故选A

练习册系列答案
相关题目
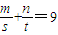 ,其中m、n是常数,当s+t取最小值
,其中m、n是常数,当s+t取最小值 时,m、n对应的点(m,n)是双曲线
时,m、n对应的点(m,n)是双曲线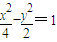 一条弦的中点,则此弦所在的直线方程为 .
一条弦的中点,则此弦所在的直线方程为 .