题目内容
 已知某程序框图如图所示
已知某程序框图如图所示①写出y=f(x)的表达式
②若f(x)-m2+m≥0对于一切x∈R均成立,求实数m的取值范围.
分析:①根据图中的条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P是否成立,选择不同的执行框(A框、B框),利用分段函数表示出所求即可.
②根据①中求出的函数,直接求出f(x)在R上的最小值,不等式f(x)-m2+m≥0对于一切x∈R均成立,即为m2-m≤f(x)对于一切x∈R恒成立,即m2-m≤f(x)min.从而建立关于m的不等关系,则实数m的取值范围可求.
②根据①中求出的函数,直接求出f(x)在R上的最小值,不等式f(x)-m2+m≥0对于一切x∈R均成立,即为m2-m≤f(x)对于一切x∈R恒成立,即m2-m≤f(x)min.从而建立关于m的不等关系,则实数m的取值范围可求.
解答:解:①根据流程图可知是条件结构
算法执行到判断框给定的条件P是否成立,选择不同的执行框(A框、B框),
故可用分段函数表示y=f(x)=
;
②由f(x)-m2+m≥0,得m2-m≤f(x).
不等式f(x)-m2+m≥0对于一切x∈R均成立,
即为m2-m≤f(x)对于一切x∈R恒成立,即m2-m≤fmix(x).
对于f(x)=
,当x≤-1时,是减函数,故x≤-1时,f(x)≥f(-1)=3;
当x>-1时,f(x)=
=
≥
=2,
故x>-1时,f(x)≥2(当x=
时取等号)
∴函数f(x)在R上的最小值为2,即f(x)min=2.
所以m2-m≤2,解得-1≤x≤2.
所以,若f(x)-m2+m≥0对于一切x∈R均成立的实数m的取值范围[-1,2].
算法执行到判断框给定的条件P是否成立,选择不同的执行框(A框、B框),
故可用分段函数表示y=f(x)=
|
②由f(x)-m2+m≥0,得m2-m≤f(x).
不等式f(x)-m2+m≥0对于一切x∈R均成立,
即为m2-m≤f(x)对于一切x∈R恒成立,即m2-m≤fmix(x).
对于f(x)=
|
当x>-1时,f(x)=
|
22x+
|
2•(22x•
|
故x>-1时,f(x)≥2(当x=
| 1 |
| 2 |
∴函数f(x)在R上的最小值为2,即f(x)min=2.
所以m2-m≤2,解得-1≤x≤2.
所以,若f(x)-m2+m≥0对于一切x∈R均成立的实数m的取值范围[-1,2].
点评:本题主要考查了条件结构,以及分段函数,如果将程序摆在我们的面前时,我们要从识别逐个语句,整体把握,概括程序的功能.本题的②实则是分离变量的解题思想,属于基础题.

练习册系列答案
相关题目
已知某程序框图如图所示,则该程序运行后输出的结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A、-1 | ||
| B、1 | ||
| C、2 | ||
D、
|
 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )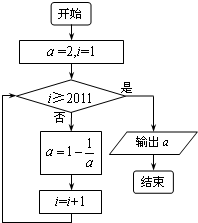 (2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( )
(2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( ) (2012•辽宁模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )
(2012•辽宁模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )