题目内容
设函数
是定义在
上的奇函数，且当
时，单调递减，若数列
是等差数列，且
，则
的值
| A．恒为正数 | B．恒为负数 | C．恒为0 | D．可正可负 |
A
解析解：∵函数f（x）是定义在R上的奇函数，
且当x≥0时，f（x）单调递减，
数列{an}是等差数列，且a3＜0，
∴a2+a4=2a3＜0，
a1+a5=2a3＜0，
x≥0，f（x）单调递减，
所以在R上，f（x）都单调递减，
因为f（0）=0，
所以x≥0时，
f（x）＜0，x＜0时，f（x）＞0，
∴f（a3）＞0
∴f（a1）+f（a5）＞0，
∴f（a2）+f（a4）＞0．
故选A．
练习册系列答案
相关题目
若函数
且
，则下列结论中，必成立的是( )
A． | B． | C． | D． |
函数
的零点所在的区间是 （ ）
| A．（-2,-1） | B．（-1,0） | C．（0,1） | D．（1,2 |
函数
在区间 [-2，4] 上是单调函数的条件是
A． | B． | C．[-1，2] | D． |
已知函数f(x)是R上的增函数，A（0，－3），B（3，1）是其图象上的两点，那么不等式－3＜f(x＋1)＜1的解集的补集是（ ）
| A．（－1，2） | B．（1，4） |
| C．（―∞，－1）∪［4，+∞） | D．（―∞，－1］∪［2，+∞） |
下列四组函数中表示相等函数的是（ ）
A． 与 | B． 与 |
C． 与 | D．  ＞  与 |
函数
的值域是（ ）
A． | B． | C． | D． |
函数
，满足（ ）
| A．是奇函数又是减函数 | B．是偶函数又是增函数 |
| C．是奇函数又是增函数 | D．是偶函数又是减 函数 |
设
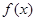为定义在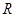
上的奇函数，当
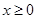时，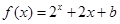
（
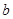为常数），则
( )
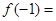| A．-3 | B．-1 | C．1 | D．3 |