题目内容
12.已知$\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(sinωx,sin(ωx+$\frac{2}{3}$π)),ω>0,f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(1)当ω=2时,求f(x)的周期和单调递增区间;
(2)若f(x)在区域[0,2π]上恰有一个最大值和一个最小值,求ω的取值范围.
分析 (1)当ω=2时,化简解析式可得f(x)=-$\sqrt{3}$sin(2x-$\frac{π}{6}$),由周期公式可求周期,由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z可解得单调递增区间.
(2)由f(x)=-$\sqrt{3}$sin(ωx-$\frac{π}{6}$),根据题意可得:$\frac{5}{4}×\frac{2π}{ω}$>2π,$\frac{3}{4}×\frac{2π}{ω}<2π$,ω>0,从而解得ω的取值范围.
解答 解:(1)∵当ω=2时,f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=sin(2x+$\frac{2}{3}$π)-sin2x=-$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x=-$\sqrt{3}$sin(2x-$\frac{π}{6}$),
∴f(x)的周期T=$\frac{2π}{2}$=π.由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z可解得单调递增区间为:[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],(k∈Z).
(2)由于f(x)=-$\sqrt{3}$sin(ωx-$\frac{π}{6}$),在区域[0,2π]上恰有一个最大值和一个最小值,
也就是$\frac{5}{4}×\frac{2π}{ω}$>2π,$\frac{3}{4}×\frac{2π}{ω}<2π$,ω>0,
从而解得:$\frac{3}{4}<ω<\frac{5}{4}$.
点评 本题主要考查了两角和与差的正弦函数公式的应用,三角函数的周期性及其求法,三角函数的图象与性质,平面向量及应用,属于基本知识的考查.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案| A. | 100种 | B. | 110种 | C. | 120种 | D. | 180种 |
| A. | [0,$\frac{16}{25}$] | B. | [-$\frac{5}{2}$,2] | C. | [-$\frac{5}{2}$,$\frac{3}{2}$] | D. | [0,$\frac{32}{25}$] |
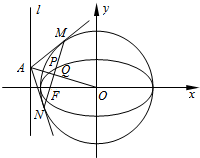 在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.
在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.