题目内容
定义域为
的可导函数
满足
且
，则
的解集为
A． | B． | C． | D． |
A
解析考点：利用导数研究函数的单调性；导数的运算；其他不等式的解法．
分析：通过已知条件，构造分数函数的导数，判断函数的单调性，通过f（2）=0，求出不等式的解集即可．
解：因为xf′（x）＞f（x），所以[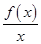
]′=[xf′（x）-f（x）]
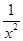＞0，
即F（x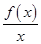）=在定义域内递增函数，又因F（2）=
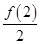=0，
则不等式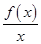＜0的解集就是不等式F（x）＜F（2）的解集，解得{x|0＜x＜2}．
故选A．
练习册系列答案
相关题目
的可导函数
满足
且
，则
的解集为(
)
(B) 
(C) 
(D) 
的可导函数
满足
且
，则
的解集为
(B)
(C)
(D) 
的可导函数
满足
且
，则
的解集为 ( )
(B) 
(C) 
(D) 
的可导函数
满足
且
，则
的解集为( )
(B) 
(C) 
(D)