题目内容
 (2012•芜湖三模)如图是某几何体的三视图,其中正视图是腰长为2a的等腰三角形,俯视图是半径为a的半圆,则该几何体的表面积是( )
(2012•芜湖三模)如图是某几何体的三视图,其中正视图是腰长为2a的等腰三角形,俯视图是半径为a的半圆,则该几何体的表面积是( )分析:三视图复原可知几何体是圆锥的一半,根据三视图数据,求出几何体的表面积.
解答: 解:由题目所给三视图可得,该几何体为圆锥的一半,
解:由题目所给三视图可得,该几何体为圆锥的一半,
那么该几何体的表面积为该圆锥表面积的一半与轴截面面积的和.
又该圆锥的侧面展开图为扇形,
所以侧面积为
×2a×2πa=2πa2,底面积为πa2,
观察三视图可知,轴截面为边长为2的正三角形,
所以轴截面面积为
×2a×2a×
=
a2,
则该几何体的表面积为
πa2+
a2.
故选C.
 解:由题目所给三视图可得,该几何体为圆锥的一半,
解:由题目所给三视图可得,该几何体为圆锥的一半,那么该几何体的表面积为该圆锥表面积的一半与轴截面面积的和.
又该圆锥的侧面展开图为扇形,
所以侧面积为
| 1 |
| 2 |
观察三视图可知,轴截面为边长为2的正三角形,
所以轴截面面积为
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则该几何体的表面积为
| 3 |
| 2 |
| 3 |
故选C.
点评:本题考查三视图求表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
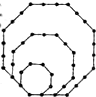 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是