题目内容
已知数列{an}满足a1=1,an+1=2an+1(n∈N*).(1)求数列{an}的通项公式；
(2)若数列{bn}满足
…
=
(n∈N*)，证明：{bn}是等差数列；
(3)证明：
-
＜
+
+…+
＜
(n∈N*).
解析：(1)∵an+1=2an+1 (n∈N*)
∴an+1+1=2(an+1)
∴{an+1}是以a1+1=2为首项，2为公比的等比数列.
∴an+1=2n，即an=2n-1(n∈N*).
(2)证法1：∵…=，∴=.
∴2［(b1+b2+…+bn)-n］=nbn, ①
2［(b1+b2+…+bn+bn+1)-(n+1)］=(n+1)bn+1. ②
②-①，得2(bn+1-1)=(n+1)bn+1-nbn,
即(n-1)bn+1-nbn+2=0, ③
nbn+2-(n+1)bn+1+2=0. ④
④-③，得nbn+2-2nbn+1+nbn=0,
即bn+2=2bn+1+bn=0,
∵bn+2-bn+1=bn+1-bn(n∈N*).
∴{bn}是等差数列.
证法2：同证法1，得(n-1)bn+1-nbn+2=0.
令n=1，得b1=2.
设b2=2+d(d∈R)，下面用数学归纳法证明bn=2+(n-1)d.
(1)当n=1,2时，等式成立.
(2)假设当n=k(k≥2)时，bk=2+(k-1)d，那么bk+1=bk-=［2+(k-1)d］-=2+［(k+1)-1］d.
这就是说，当n=k+1时，等式也成立.
根据(1)和(2)，可知bn=2+(n-1)d对任何n∈N*都成立.
∵bn+1-bn=d,∴{bn}是等差数列.
(3)证明：∵
=
=
＜
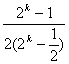，k=1,2,…,n,
∴
+
+…+
＜
.
∵
=
=
-
=
-
≥
-
·
,k=1,2,…,n,
∴
+
+…+
≥
-
(
+
+…+
)=
-
(1-
)
＞
-
.
∴
-
＜
+
+…+
＜
(n∈N*).
