题目内容

已知数列{an}满足a1=1,an+1=.

（1）计算a2,a3,a4；

（2）猜测an的表达式并用数学归纳法证明.

思路分析：首先通过计算a2，a3，a4，然后猜想an的表达式，最后通过数学归纳法来证明.

(1)解：由an+1=及a1=1，得

a2=,进而a3=,a4==.

(2)证明：猜想an=,面用数学归纳法证明之.

当n=1时，a1=,=1,而已知a1=1,

∴n=1时，猜想正确.

假设当n=k时，猜想正确，即ak=,

则n=k+1时，ak+1=.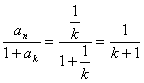

∴当n=k+1时，猜想也成立.

综上所述可知，对一切n∈N,猜想an=都正确.

练习册系列答案
相关题目
已知数列{an}满足：a1=1且an+1=
3+4an
12-4an
， n∈N*．
（1）若数列{bn}满足：bn=
1
an-
1
2
(n∈N*)，试证明数列bn-1是等比数列；
（2）求数列{anbn}的前n项和Sn；
（3）数列{an-bn}是否存在最大项，如果存在求出，若不存在说明理由．
已知数列{an}满足
1
2
a1+
1
22
a2+
1
23
a3+…+
1
2n
an=2n+1则{an}的通项公式
 
．
已知数列{an}满足：a1=
3
2
，且an=
3nan-1
2an-1+n-1
（n≥2，n∈N*）．
（1）求数列{an}的通项公式；
（2）证明：对于一切正整数n，不等式a1•a2•…an＜2•n！
已知数列{an}满足an+1=|an-1|（n∈N*）
（1）若a1=
54
，求an；
（2）若a1=a∈（k，k+1），（k∈N*），求{an}的前3k项的和S3k（用k，a表示）
（2012•北京模拟）已知数列{an}满足an+1=an+2，且a1=1，那么它的通项公式an等于
2n-1
2n-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网