题目内容
已知函数f（x）=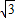
asinx+bcos（x-
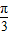）的图象经过点（
），（
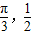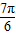，0）．（1）求实数a，b的值；
（2）求函数f（x）的周期及单调增区间．
【答案】分析：（1）由函数的图象经过点（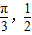
），（
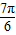，0），建立方程，即可求得实数a，b的值；
（2）先将函数化简为f（x）=sin（2x-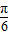
），由此可求函数f（x）的周期及单调增区间．
解答：解：（1）∵函数f（x）=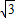
asinx+bcos（x-
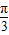）的图象经过点（
），（
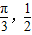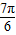，0）．
∴
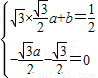------（3分）
∴a=1，b=-1------（6分）
（2）由（1）知：函数f（x）=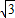
asinx+bcos（x-
）=
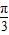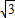sinx-cos（x-
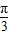）=sin（x-
）
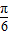∴函数f（x）的周期T=2π （10分）
由2kπ-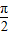
≤x-
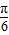≤2kπ+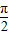
，解得2kπ-
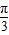≤x≤2kπ+
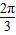，k∈Z．
即函数的增区间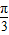[2kπ-
，2kπ+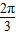
]k∈Z．（12分）
点评：本题考查三角函数的化简，考查三角函数的性质，考查学生的计算能力，正确化简函数是关键．
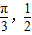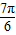），（，0），建立方程，即可求得实数a，b的值；（2）先将函数化简为f（x）=sin（2x-
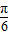），由此可求函数f（x）的周期及单调增区间．解答：解：（1）∵函数f（x）=
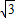asinx+bcos（x-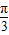）的图象经过点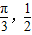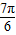（），（，0）．∴
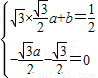------（3分）∴a=1，b=-1------（6分）
（2）由（1）知：函数f（x）=
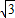asinx+bcos（x-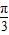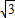）=sinx-cos（x-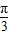）=sin（x-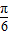）∴函数f（x）的周期T=2π （10分）
由2kπ-
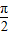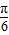≤x-≤2kπ+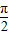，解得2kπ-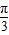≤x≤2kπ+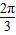，k∈Z．即函数的增区间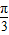[2kπ-
，2kπ+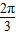]k∈Z．（12分）点评：本题考查三角函数的化简，考查三角函数的性质，考查学生的计算能力，正确化简函数是关键．
练习册系列答案
相关题目