题目内容
(本题满分12分)已知圆 关于
关于 轴对称,经过抛物线
轴对称,经过抛物线 的焦点,且被直线
的焦点,且被直线 分成两段弧长之比为1∶2,求圆
分成两段弧长之比为1∶2,求圆 的方程.
的方程.
 或
或 .
.
解析试题分析:求圆的方程有两种方法①几何法,通过研究圆的性质进而求出圆的基本量.②代数法,即设出圆的方程,用待定系数法求解,利用待定系数法的关键是建立关于a,b,r或D,E,F的方程组.本题采用代数法,直接设出圆的方程,再根据已知条件解出参数.
试题解析:设圆 的方程为
的方程为
 抛物线
抛物线 的焦点F(1,0)
的焦点F(1,0)  ① 4分
① 4分
又直线 分圆的两段弧长之比为1:2,可知圆心到直线
分圆的两段弧长之比为1:2,可知圆心到直线 的距离等于半径的
的距离等于半径的
即 ② 8分
② 8分
解①②得 故所求圆的方程为
故所求圆的方程为  或
或 12分
12分
考点:圆的方程及点到直线的距离公式、抛物线.

练习册系列答案
相关题目
已知直线
 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
| A.1 | B.2 | C. | D.4 |
已知圆 与圆
与圆 相外切, 则
相外切, 则 的最大值为 ( )
的最大值为 ( )
A. | B. | C. | D. |
如果圆 上总存在到原点的距离为
上总存在到原点的距离为 的点,
的点,
则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
| C.[-1, 1] | D. |
曲线 为参数)的对称中心( )
为参数)的对称中心( )
| A.在直线y=2x上 | B.在直线y=-2x上 |
| C.在直线y=x-1上 | D.在直线y=x+1上 |
下面一段程序执行后输出结果是( )
A=2
A=A*2
A=A+6
PRINT A
| A.2 | B.8 | C.10 | D.18 |
 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= .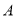 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.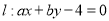 平分圆
平分圆 的距离的最大值;
的距离的最大值;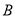 平分圆
平分圆 的前
的前 项和为
项和为 ,且
,且 ,数列
,数列 满足
满足 .
. 满足
满足 ,其前
,其前 ,求
,求