题目内容
命题p:方程2x2+mx-2m2-5m-3=0有一正根一负根;
命题q:函数f(x)=x3+mx2+(m+
)x+6在R上有极值;
若命题“p或q”为真,“p且q”为假,求实数m的取值范围.
命题q:函数f(x)=x3+mx2+(m+
| 4 |
| 3 |
若命题“p或q”为真,“p且q”为假,求实数m的取值范围.
对命题p,令f(x)=2x2+mx-2m2-5m-3,则f(0)<0,即2m2+5m+3>0,解得m<-
或m>-1; (4分)
当命题q为真时:f′(x)=3x2+2mx+(m+
)△=4m2-12(m+
)>0(6分)∴m2-3m-4>0
故m>4或m<-1 (8分)
当命题p或q为真,p且q为假,即p与q有且仅有一个成立∴
或
(10分)
∴m∈[-
,-1)∪(-1,4].(12分)
| 3 |
| 2 |
当命题q为真时:f′(x)=3x2+2mx+(m+
| 4 |
| 3 |
| 4 |
| 3 |
故m>4或m<-1 (8分)
当命题p或q为真,p且q为假,即p与q有且仅有一个成立∴
|
|
∴m∈[-
| 3 |
| 2 |

练习册系列答案
相关题目
 x+3=0的两根都是实数,q:方程2x2-2
x+3=0的两根都是实数,q:方程2x2-2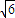 x+3=0的两根都是实数,q:方程2x2-2
x+3=0的两根都是实数,q:方程2x2-2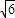 x+3=0的两根不相等,试写出由这组命题构成的“p或q”、“p且q”、“非p”形式的复合命题,并指出其真假.
x+3=0的两根不相等,试写出由这组命题构成的“p或q”、“p且q”、“非p”形式的复合命题,并指出其真假.