题目内容
已知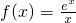 ,给定正的常数k,解不等式f′(x)+k(1-x)f(x)>0.
,给定正的常数k,解不等式f′(x)+k(1-x)f(x)>0.
解:∵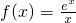 ,∴f′(x)=
,∴f′(x)=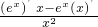 =
= ,
,
不等式f′(x)+k(1-x)f(x)>0可化为,
 +k(1-x)
+k(1-x)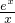 >0,即
>0,即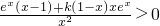
变形得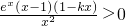 ,即
,即 ,
,
只需(x-1)(kx-1)<0,对应方程的两根分别为1,
当0<k<1时,1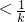 ,解得1
,解得1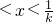 ;
;
当k=1时,1= ,不等式无解;
,不等式无解;
当k>1时,1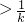 ,解得
,解得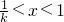 .
.
故不等式f′(x)+k(1-x)f(x)>0的解集为:
当0<k<1时,{x|1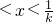 };
};
当k=1时,空集;
当k>1时,{x|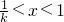 }.
}.
分析:本题先要求对商的导数,再代入已知不等式,通过通分等手段化为(x-1)(kx-1)<0,然后针对k进行分类讨论,当0<k<1时,1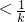 ,解得1
,解得1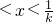 ;当k=1时,1=
;当k=1时,1= ,不等式无解;当k>1时,1
,不等式无解;当k>1时,1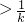 ,解得
,解得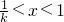 ,注意最后写成集合的形式.
,注意最后写成集合的形式.
点评:本题为不等式的解法与函数导数的结合,注意不等式的等价转化,注意在解不等式(x-1)(kx-1)<0时,对k的讨论,属中档题.
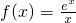 ,∴f′(x)=
,∴f′(x)=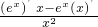 =
= ,
,不等式f′(x)+k(1-x)f(x)>0可化为,
 +k(1-x)
+k(1-x)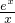 >0,即
>0,即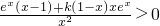
变形得
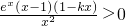 ,即
,即 ,
,只需(x-1)(kx-1)<0,对应方程的两根分别为1,

当0<k<1时,1
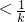 ,解得1
,解得1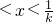 ;
;当k=1时,1=
 ,不等式无解;
,不等式无解;当k>1时,1
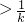 ,解得
,解得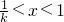 .
.故不等式f′(x)+k(1-x)f(x)>0的解集为:
当0<k<1时,{x|1
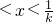 };
};当k=1时,空集;
当k>1时,{x|
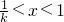 }.
}.分析:本题先要求对商的导数,再代入已知不等式,通过通分等手段化为(x-1)(kx-1)<0,然后针对k进行分类讨论,当0<k<1时,1
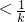 ,解得1
,解得1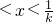 ;当k=1时,1=
;当k=1时,1= ,不等式无解;当k>1时,1
,不等式无解;当k>1时,1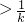 ,解得
,解得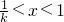 ,注意最后写成集合的形式.
,注意最后写成集合的形式.点评:本题为不等式的解法与函数导数的结合,注意不等式的等价转化,注意在解不等式(x-1)(kx-1)<0时,对k的讨论,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”.
是与n无关的非零常数t=f(k),则称该数列{an}是“k类和科比数列”. ,求数列{an}的通项公式;
,求数列{an}的通项公式;