题目内容
设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象为
- A.

- B.

- C.

- D.

B
分析:先对函数f(x)进行求导运算,根据在点(t,f(t))处切线的斜率为在点(t,f(t))处的导数值,可得答案.
解答:∵f(x)=x sinx+cosx
∴f'(x)=(x sinx)'+(cosx)'
=x(sinx)'+(x)'sinx+(cosx)'
=x cosx+sinx-sinx
=x cosx
∴k=g(t)=tcost
根据y=cosx的图象可知g(t)应该为奇函数且当x>0时g(t)>0
故选B.
点评:本题主要考查函数的导数和在某点处切线斜率的关系.属基础题.
分析:先对函数f(x)进行求导运算,根据在点(t,f(t))处切线的斜率为在点(t,f(t))处的导数值,可得答案.
解答:∵f(x)=x sinx+cosx
∴f'(x)=(x sinx)'+(cosx)'
=x(sinx)'+(x)'sinx+(cosx)'
=x cosx+sinx-sinx
=x cosx
∴k=g(t)=tcost
根据y=cosx的图象可知g(t)应该为奇函数且当x>0时g(t)>0
故选B.
点评:本题主要考查函数的导数和在某点处切线斜率的关系.属基础题.

练习册系列答案
相关题目
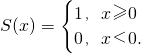 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).