题目内容

已知椭圆的焦点为，，且经过点.

（Ⅰ）求椭圆的方程；

（Ⅱ）设过的直线与椭圆交于、两点，问在椭圆上是否存在一点，使四边形为平行四边形，若存在，求出直线的方程，若不存在，请说明理由.

（Ⅰ）                  ………………………………3分

，                                  ………………………………5分

 椭圆的方程为                    ………………………………7分

（Ⅱ）假设存在符合条件的点,

设直线的方程为                     ………………………………8分

由得:，

，                          

 的中点为              ………………………………10分

四边形为平行四边形

与的中点重合，即：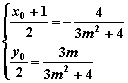

                        ………………………………13分

把点坐标代入椭圆的方程得:

解得                                    ………………………………14分

存在符合条件的直线的方程为： ………………………………15分

练习册系列答案
相关题目
已知椭圆的焦点为F1（-1，0），F2（1，0），直线l：x-y+5=0，则
（1）经过直线l上一点P且长轴长最短的椭圆方程为
 
，（2）点P的坐标是
 
．
（1）已知椭圆的焦点为F1（0，-5），F2（0，5），点P（3，4）在椭圆上，求它的方程
（2）已知双曲线顶点间的距离为6，渐近线方程为y=±
32
x，求它的方程．
已知椭圆的焦点为F1（-6，0），F2（6，0），且该椭圆过点P（5，2）．
（1）求椭圆的标准方程
（2）若椭圆上的点M（x0，y0）满足MF1⊥MF2，求y0的值．
已知椭圆的焦点为F1（-t，0），F2（t，0），（t＞0），P为椭圆上一点，且|F1F2|是|PF1|，|PF2|的等差中项．
（1）求椭圆方程；
（2）如果点P在第二象限且∠PF1F2=1200，求tan∠F1PF2的值；
（3）设A是椭圆的右顶点，在椭圆上是否存在点M（不同于点A），使∠F1MA=90°，若存在，请求出点M的坐标；若不存在，请说明理由．
已知椭圆的焦点为F1(0，-2
2
)，F2(0，2
2
)，离心率为e，已知
2
3
，e，
4
3
成等比数列；
（1）求椭圆的标准方程；
（2）已知P为椭圆上一点，求
PF1
•
PF2
最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网