题目内容

7．已知i是虚数单位，若$\frac{3+i}{z}=1-i$，则z在复平面内对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 根据复数的几何意义进行化简求解．

解答 解：由$\frac{3+i}{z}=1-i$，得z=$\frac{3+i}{1-i}$=$\frac{（3+i）（1+i）}{（1-i）（1+i）}=\frac{2+4i}{2}$=1+2i．
对应的坐标为（1，2），位于第一象限，
故选：A

点评 本题主要考查复数的几何意义，根据复数的基本运算先进行化简是解决本题的关键．

练习册系列答案
相关题目
17．已知a是实数，函数f（x）=2ax2+2x-3在x∈[-1，1]上恒小于零，求实数a的取值范围．
18．已知sinθ=-$\frac{2\sqrt{6}}{5}$，π＜θ＜$\frac{3π}{2}$．
（Ⅰ）求cosθ，tanθ的值；
（Ⅱ）求[sin（$\frac{θ}{2}$+π）+sin（$\frac{θ}{2}$+$\frac{π}{2}$）]•[cos（$\frac{3π}{2}$-$\frac{θ}{2}$）+cos（$\frac{θ}{2}$-5π）]的值．
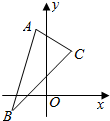15．已知平行四边形ABCD的三个顶点的坐标为A（-1，4），B（-2，-1），C（2，3）．
（1）求平行四边形ABCD的顶点D的坐标
（2）在△ACD中，求CD边上的高线所在直线方程；
（3）求△ACD的面积．
2．已知函数f（x）=x2+（a-4）x+3-a
（1）若f（x）≤0在区间[0，1]上恒成立，求a的取值范围；
（2）若对于任意的a∈（0，4），存在x1，x2∈[0，2]，使得||f（x1）|-|f（x2）||≥t，求t的取值范围．
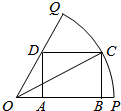12．如图，已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形，C是该扇形弧上的动点，ABCD是扇形的内接矩形，记∠BOC为α．
（Ⅰ）若Rt△CBO的周长为$\frac{{\sqrt{7}（2\sqrt{10}+5）}}{5}$，求$\frac{3-cos2α}{co{s}^{2}α-sinαcosα}$的值．
（Ⅱ）求$\overrightarrow{OA}•\overrightarrow{AB}$的最大值，并求此时α的值．
19．已知向量$\overrightarrow{a}$≠$\overrightarrow{b}$，|$\overrightarrow{b}$|=1．
（1）若|$\overrightarrow{a}$|=2，|$\overrightarrow{a}$+$\overrightarrow{b}$|=2|$\overrightarrow{a}$-$\overrightarrow{b}$|，求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦；
（2）对任意实数t，恒有|$\overrightarrow{a}$-t$\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\overrightarrow{b}$|，求证：（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{b}$．
16．设函数f（x）=|x-$\frac{5}{2}$|+|x-a|，x∈R．
（Ⅰ）求证：当a=-$\frac{1}{2}$时，不等式f（x）≥3成立；
（Ⅱ）关于x的不等式f（x）≥a在R上恒成立，求实数a的最大值．
17．若$cos（2π-α）=\frac{{2\sqrt{2}}}{3}$，且$α=（-\frac{π}{2}，0）$，则sin（π+α）=$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网