Question

如图，三棱锥P-ABC中，PB⊥底面ABC，AC⊥BC，PB=BC=AC，点E、F分别是PC、PA的中点．
（Ⅰ）求证：PC⊥平面BEF；
（Ⅱ）求二面角A-EB-F的大小．

Answer 1

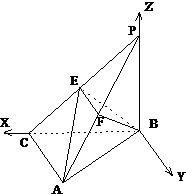方法（一）
（Ⅰ）证明：由已知可得△PBC为等腰直角三角形，则BE⊥PC．    
由PB⊥平面ABC，AC?平面ABC，则PB⊥AC．
又AC⊥BC，BC∩PB=B，
则AC⊥平面PBC，由PC?平面PBC，得AC⊥PC． 
由中位线定理得，EF∥CA，于是EF⊥PC，又BE∩EF=E，
所以PC⊥平面BEF．           
（Ⅱ）解：由第（Ⅰ）问，已证明AC⊥平面PBC，又BE?平面PBC，
则AC⊥BE．已证明BE⊥PC，又PC∩AC=C，则BE⊥平面PAC．
因为EF?平面PAC，AE?平面PAC，所以BE⊥EF，BE⊥AE．
由二面角的定义，得∠AEF为二面角A-EB-F的平面角．
设PB=BC=AC=2，则，，
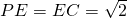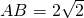在Rt△PAB中，PB=2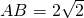，，所以，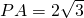
在Rt△ACE中，AC=2，，∴，
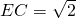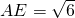在△AEF中，由余弦定理得，．
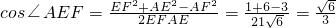则二面角A-EB-F的大小为．        
方法（二）
如图建立空间直角坐标系，设PB=BC=AC=2，可求出以下各点的坐标：A（2，2，0），B（0，0，0），C（2，0，0），
P（0，0，2），E（1，0，1），F（1，1，1）
（Ⅰ），，
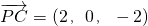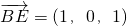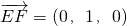
有，，
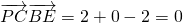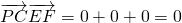于是PC⊥BE，PC⊥EF，又BE∩EF=E，则PC⊥平面BEF．          
（Ⅱ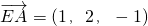），有，，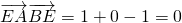
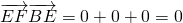于是EA⊥BE，EF⊥BE，由二面角定义，向量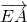与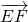的夹角为所求．
∴，
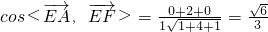所以二面角A-EB-F的大小为．   
分析：方法一：（Ⅰ）利用线面垂直的判定定理，证明BE⊥PC，EF⊥PC，即可得到PC⊥平面BEF；
（Ⅱ）先判断∠AEF为二面角A-EB-F的平面角，再在△AEF中，利用余弦定理，可求二面角A-EB-F的大小；
方法（二）：向量法，建立坐标系，用坐标表示点，用坐标表示向量
（Ⅰ）证明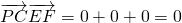，从而可证PC⊥平面BEF；
（Ⅱ）先判断向量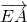与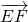的夹角为所求，再利用向量夹角公式，即可求得二面角A-EB-F的大小．
点评：本小题主要考查三棱锥，直线与平面的垂直，二面角的计算，考查空间想象能力、思维能力和运算能力．两法并举，既展现传统方法，又体现向量法的优点．