题目内容
已知数列{an}满足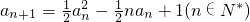 ,且a1=3.
,且a1=3.
(1)计算a2,a3,a4的值,由此猜想数列{an}的通项公式;
(2)用数学归纳法对你的结论进行证明.
解:(1)∵a1=3,an+1=
 -
- nan+1(n∈N*),
nan+1(n∈N*),
∴a2= ×9-
×9- ×1×3+1=4,
×1×3+1=4,
同理可求a3=5,a4=6,猜想:an=n+2(n∈N*);
(2)①当n=1时,a1=3,结论成立;
②假设当n=k(k≥1,k∈N*)时,结论成立,即ak=k+2,
则当n=k+1时,ak+1=
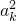 -
- kak+1=
kak+1= (k+2)2-
(k+2)2- k(k+2)+1=
k(k+2)+1= (k+2)[k+2-k]+1=k+3=(k+1)+1,
(k+2)[k+2-k]+1=k+3=(k+1)+1,
即当n=k+1时,结论也成立.
由①②得,数列{an}的通项公式为an=n+2(n∈N*).
分析:(1)a1=3,an+1=
 -
- nan+1(n∈N*),将n=1,2,3代入上式计算,猜想即可;
nan+1(n∈N*),将n=1,2,3代入上式计算,猜想即可;
(2)对于an=n+2(n∈N*),用数学归纳法证明即可.①当n=1时,证明结论成立,②假设当n=k(k≥1,k∈N*)时,结论成立,利用归纳假设,去证明当n=k+1时,结论也成立即可.
点评:本题考查数学归纳法,猜得an=n+2(n∈N*)是关键,考查归纳推理与论证的能力,属于中档题.

 -
- nan+1(n∈N*),
nan+1(n∈N*),∴a2=
 ×9-
×9- ×1×3+1=4,
×1×3+1=4,同理可求a3=5,a4=6,猜想:an=n+2(n∈N*);
(2)①当n=1时,a1=3,结论成立;
②假设当n=k(k≥1,k∈N*)时,结论成立,即ak=k+2,
则当n=k+1时,ak+1=

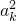 -
- kak+1=
kak+1= (k+2)2-
(k+2)2- k(k+2)+1=
k(k+2)+1= (k+2)[k+2-k]+1=k+3=(k+1)+1,
(k+2)[k+2-k]+1=k+3=(k+1)+1,即当n=k+1时,结论也成立.
由①②得,数列{an}的通项公式为an=n+2(n∈N*).
分析:(1)a1=3,an+1=

 -
- nan+1(n∈N*),将n=1,2,3代入上式计算,猜想即可;
nan+1(n∈N*),将n=1,2,3代入上式计算,猜想即可;(2)对于an=n+2(n∈N*),用数学归纳法证明即可.①当n=1时,证明结论成立,②假设当n=k(k≥1,k∈N*)时,结论成立,利用归纳假设,去证明当n=k+1时,结论也成立即可.
点评:本题考查数学归纳法,猜得an=n+2(n∈N*)是关键,考查归纳推理与论证的能力,属于中档题.

练习册系列答案
相关题目