题目内容
已知奇函数f(x)是定义在(-1,1)上的增函数,若f(m-1)+f(2m-1)≤0,则m的取值范围是
- A.
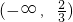
- B.

- C.

- D.
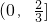
D
分析:根据题意,对f(m-1)+f(2m-1)≤0变形,结合奇函数的性质可得f(m-1)≤f(1-2m),由函数的定义域与单调性可得结论.
解答:∵f(m-1)+f(2m-1)≤0,
∴f(m-1)≤-f(2m-1),
又∵f(x)为奇函数,则-f(2m-1)=f(1-2m),
则有f(m-1)≤f(1-2m),
∵f(x)为(-1,1)上的增函数,
∴
∴0<m≤
故选D.
点评:本题考查函数奇偶性与单调性的综合应用,解题时需要注意函数的定义域.
分析:根据题意,对f(m-1)+f(2m-1)≤0变形,结合奇函数的性质可得f(m-1)≤f(1-2m),由函数的定义域与单调性可得结论.
解答:∵f(m-1)+f(2m-1)≤0,
∴f(m-1)≤-f(2m-1),
又∵f(x)为奇函数,则-f(2m-1)=f(1-2m),
则有f(m-1)≤f(1-2m),
∵f(x)为(-1,1)上的增函数,
∴

∴0<m≤

故选D.
点评:本题考查函数奇偶性与单调性的综合应用,解题时需要注意函数的定义域.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目