题目内容
侧棱长为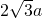 的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为
的正三棱锥V-ABC的侧棱间的夹角为40°,过顶点A作截面AEF,截面AEF的最小周长为
- A.
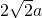
- B.6a
- C.4a
- D.

B
分析:画出几何体的图形,推出截面周长最小值的情形,确定展开图的有关的角,利用余弦定理求出距离即可.
解答: 解:如图三棱锥以及侧面展开图,要求截面AEF的周长最小,就是侧面展开图中AG的距离,
解:如图三棱锥以及侧面展开图,要求截面AEF的周长最小,就是侧面展开图中AG的距离,
因为侧棱长为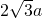 的正三棱锥V-ABC的侧棱间的夹角为40°,∠AVG=120°,
的正三棱锥V-ABC的侧棱间的夹角为40°,∠AVG=120°,
所以由余弦定理可知AG2=VA2+VG2-2VA•VGcos120°
=
=3 .
.
AG=6a.
故选B.
点评:本题是中档题,考查几何体的侧面展开图距离的最小值问题,余弦定理的应用,考查空间想象能力,计算能力,转化思想.
分析:画出几何体的图形,推出截面周长最小值的情形,确定展开图的有关的角,利用余弦定理求出距离即可.
解答:
 解:如图三棱锥以及侧面展开图,要求截面AEF的周长最小,就是侧面展开图中AG的距离,
解:如图三棱锥以及侧面展开图,要求截面AEF的周长最小,就是侧面展开图中AG的距离,因为侧棱长为
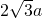 的正三棱锥V-ABC的侧棱间的夹角为40°,∠AVG=120°,
的正三棱锥V-ABC的侧棱间的夹角为40°,∠AVG=120°,所以由余弦定理可知AG2=VA2+VG2-2VA•VGcos120°
=

=3
 .
.AG=6a.
故选B.
点评:本题是中档题,考查几何体的侧面展开图距离的最小值问题,余弦定理的应用,考查空间想象能力,计算能力,转化思想.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
侧棱长为
 的正三棱锥V-ABC的各侧棱间的夹角为60°,过AB作截面AOB,则截面△AOB的最小周长为
的正三棱锥V-ABC的各侧棱间的夹角为60°,过AB作截面AOB,则截面△AOB的最小周长为
[
]|
A . |
B .6a |
|
C . |
D .9a |
 的正三棱锥V-ABC的各侧棱间的夹角为60°,过AB作截面AOB,则截面△AOB的最小周长为
的正三棱锥V-ABC的各侧棱间的夹角为60°,过AB作截面AOB,则截面△AOB的最小周长为

 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 ,
的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=400 , 
 的正三棱锥V—ABC中,
的正三棱锥V—ABC中, ,过A作截面AEF,则截面三角形AEF周长的最小值是______________
,过A作截面AEF,则截面三角形AEF周长的最小值是______________