题目内容
已知f（x）是定义在（0，+∞）上的可导函数，且满足xf′（x）-f（x）≥0，对任意正数a，b，若a＞b，则必有
- A.af（a）≤bf（b）
- B.bf（b）≤af（a）
- C.af（b）≤bf（a）
- D.bf（a）≤af（b）
C
分析：令F（x）=
，对其进行求导，根据xf′（x）-f（x）≥0，证明F（x）是增函数，利用单调性进行求解；
解答：F（x）=，
可得F'（x）=
[xf′（x）-f（x）]，
∴xf′（x）-f（x）＞0 所以 F'（x）＞0 即F（x）是增函数，
即当a＞b＞0时，F（a）＞F（b），
∴
≤
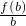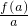，从而af（b）≤bf（a）．
故选C；
点评：本题考查函数的单调性和导数的关系，解题时要认真审题，注意导数的合理运用．
分析：令F（x）=
，对其进行求导，根据xf′（x）-f（x）≥0，证明F（x）是增函数，利用单调性进行求解；解答：F（x）=
，可得F'（x）=
[xf′（x）-f（x）]，∴xf′（x）-f（x）＞0 所以 F'（x）＞0 即F（x）是增函数，
即当a＞b＞0时，F（a）＞F（b），
∴
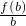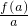≤，从而af（b）≤bf（a）．故选C；
点评：本题考查函数的单调性和导数的关系，解题时要认真审题，注意导数的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目