题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:由已知可得f‘(1)=0…………………………………………………………1分 又 f‘(1)=1+2b+c=0,………………………………………………………………2分 将b=-2代入,可得c=3………………………………………………………………3分 |
(2) |
解:可知 令 又当-1<x<1时, 如图所示;
易知c≥3…………………………8分 |
(3) |
解:若1≤-b≤3,则
又1+2b+c=0,得b=-2或b=0(舍),c=3, 若-b≥3,则 =9+6b+c=-1,又1+2b+c=0 得 综上所述,b=-2,c=3…………………………………………14分 |

练习册系列答案
相关题目

 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.  且函数f(x)的最小正周期为
且函数f(x)的最小正周期为 .
. 且
且 ,试求
,试求 的值.
的值. 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在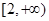 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.  且此函数图象过点(1, 5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1, 5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.