Question

如图5，正方体的棱长为a，

E为DD₁的中点.

（1）求证：BD₁//平面EAC；

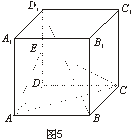（2）求点D₁到平面EAC的距离．

Answer 1

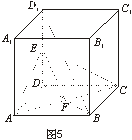（1）证明：如图5，连接BD交AC于F，连EF.  （1分）

因为F为正方形ABCD对角线的交点，

所长F为AC、BD的中点.                      （3分）

在DDD₁B中，E、F分别为DD₁、DB的中点，

所以EF//D₁B.                                （5分）

又EFÌ平面EAC，所以BD₁//平面EAC.           （7分）

（2）解1：设D₁到平面EAC的距离为d.

在DEAC中，EF^AC，且，，

所以，

于是.                    （9分）

因为，  （11分）

又，即，             （13分）

解得，故D₁到平面EAC的距离为.    （14分）

解2：因为，，所以平面

      又平面ACE，故平面平面ACE

      过D作DM，交EF和于M和G，所以MG平面ACE（9分）

      由（1）可知，所以GM是到平面ACE的距离，也就是到平面ACE的距离（10分）

     在中，因为，即

所以，,（13分）

故,即D₁到平面EAC的距离为.    （14分）

解3：因为，F为AC这中点，所以且

     设到平面ACE的距离为d,

     因为，即

     也就是，所以

     因为到平面ACE的距离与到平面ACE的距离相等，

     所以，D₁到平面EAC的距离为.    （10分）