题目内容
已知数列{an}为等差数列,a3=3,a1+a2+…+a6=21,数列(
)的前n项和为Sn,若对一切n∈N*,恒有S2n-Sn>
,则m能取到的最大正整数是______.
| 1 |
| an |
| m |
| 16 |
设数列{an}的公差为d,由题意得,
,解得
,
∴an=n,且
=
,
∴Sn=1+
+
+…+
,
令Tn=S2n-Sn=
+
+…+
,
则Tn+1=
+
+…+
,
即Tn+1-Tn=
+
-
>
+
-
=0
∴Tn+1>Tn,
则Tn随着n的增大而增大,即Tn在n=1处取最小值,
∴T1=S2-S1=
,
∵对一切n∈N*,恒有S2n-Sn>
成立,
∴
>
即可,解得m<8,
故m能取到的最大正整数是7.
|
|
∴an=n,且
| 1 |
| an |
| 1 |
| n |
∴Sn=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
令Tn=S2n-Sn=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
则Tn+1=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+2 |
即Tn+1-Tn=
| 1 |
| 2n+2 |
| 1 |
| 2n+1 |
| 1 |
| n+1 |
| 1 |
| 2n+2 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
∴Tn+1>Tn,
则Tn随着n的增大而增大,即Tn在n=1处取最小值,
∴T1=S2-S1=
| 1 |
| 2 |
∵对一切n∈N*,恒有S2n-Sn>
| m |
| 16 |
∴
| 1 |
| 2 |
| m |
| 16 |
故m能取到的最大正整数是7.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

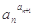 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4