题目内容
已知抛物线C:x2=2py(p>0)的焦点为F,定点A(3,2)与点F在C的两侧,C上的动点P到点A的距离与到其准线l的距离之和的最小值为 。
。
(1)求抛物线C的方程;
(2)设准线l与y轴交于点M,过点M作直线与C交于P,Q两点,Q关于y轴的对称点为Q'。
①求证:Q',F,P共线;
②求△MPQ'面积S的取值范围。
 。
。(1)求抛物线C的方程;
(2)设准线l与y轴交于点M,过点M作直线与C交于P,Q两点,Q关于y轴的对称点为Q'。
①求证:Q',F,P共线;
②求△MPQ'面积S的取值范围。
解:(1)过P作PP1⊥l于P1,
则|PA|+|PP1|=|PA|+|PF|≥|AF|
当P,A,F共线时,|PA|+|PP1|取最小值
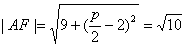
解得p=6,或p=2
当p=6时,抛物线C的方程为x2=12y,
此时,点A与点F在抛物线C同侧,这与已知不符
∴p=2,
抛物线C的方程为x2=4y。
(2)①设直线PQ的方程为y=kx-1,
由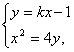 消去y,整理得x2-4kx+4=0,
消去y,整理得x2-4kx+4=0,
由Δ=16k2-16>0,得|k|>1
由P(x1,y1),Q(x2,y2),
则Q'(-x2,y2),x1+x2=4k,x1·x2=4
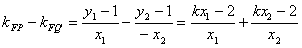
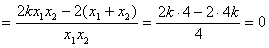
∴Q',F,P共线
②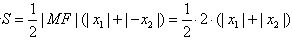
=|x1+x2|=4|k|,
∵|k|>1
∴S>1。
则|PA|+|PP1|=|PA|+|PF|≥|AF|
当P,A,F共线时,|PA|+|PP1|取最小值
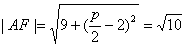
解得p=6,或p=2
当p=6时,抛物线C的方程为x2=12y,
此时,点A与点F在抛物线C同侧,这与已知不符
∴p=2,
抛物线C的方程为x2=4y。
(2)①设直线PQ的方程为y=kx-1,
由
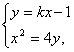 消去y,整理得x2-4kx+4=0,
消去y,整理得x2-4kx+4=0,由Δ=16k2-16>0,得|k|>1
由P(x1,y1),Q(x2,y2),
则Q'(-x2,y2),x1+x2=4k,x1·x2=4
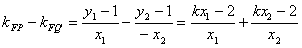
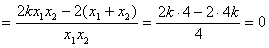
∴Q',F,P共线
②
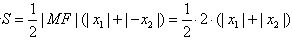
=|x1+x2|=4|k|,
∵|k|>1
∴S>1。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目