题目内容
(本小题满分12分)已知椭圆![]() 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点![]() ,离心率
,离心率![]() ,
,![]() 为右焦点,过焦点
为右焦点,过焦点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点(不同于点
两点(不同于点![]() ).(1)求椭圆
).(1)求椭圆![]() 的方程;(2)当
的方程;(2)当![]() 时,求直线PQ的方程;(3)判断
时,求直线PQ的方程;(3)判断![]() 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() 或
或![]() (Ⅲ)不可能是等边三角形
(Ⅲ)不可能是等边三角形
解析:
(Ⅰ)设椭圆方程为![]() (a>b>0) ,
(a>b>0) ,
由已知 ![]() ∴
∴![]() ……2分
……2分
∴ 椭圆方程为![]() . 3分
. 3分
(Ⅱ)解法一 椭圆右焦点![]() . 设直线
. 设直线![]()
![]() 方程为
方程为![]() (
(![]() ∈R). …4分
∈R). …4分
由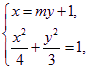 得
得![]() .①显然,方程①的
.①显然,方程①的![]() .
.
设![]() ,则有
,则有![]() .
.
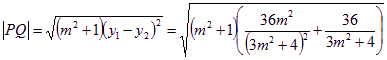
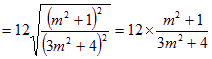 .…6分∵
.…6分∵![]() ,∴
,∴ ![]() .
.
解得![]() .∴直线PQ 方程为
.∴直线PQ 方程为![]() ,即
,即![]() 或
或![]() .…8分
.…8分
解法二: 椭圆右焦点![]() .当直线的斜率不存在时,
.当直线的斜率不存在时,![]() ,不合题意……4分
,不合题意……4分
设直线![]()
![]() 方程为
方程为![]() , 由
, 由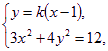 得
得![]() .①
.①
显然,方程①的![]() .设
.设![]() ,
,
则![]() .
. ![]()
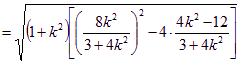 =
=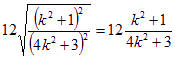 .…6分
.…6分
∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() 或
或![]() .………………8分
.………………8分
(Ⅲ)![]() 不可能是等边三角形. 如果
不可能是等边三角形. 如果![]() 是等边三角形,必有
是等边三角形,必有![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,或
,或![]() (无解).…10分 而当
(无解).…10分 而当![]() 时,
时,![]() ,不能构成等边三角形.∴
,不能构成等边三角形.∴![]() 不可能是等边三角形.…12分
不可能是等边三角形.…12分

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目