题目内容
设动点M(x,y)(x≥0)到定点F(2,0)的距离比它到y轴的距离大2.
(Ⅰ)求动点M的轨迹方程C;
(Ⅱ)设过点F的直线l交曲线C于A,B两点,O为坐标原点,求△AOB面积的最小值.
(Ⅰ)求动点M的轨迹方程C;
(Ⅱ)设过点F的直线l交曲线C于A,B两点,O为坐标原点,求△AOB面积的最小值.
分析:(I)依题意知,动点M到定点F(2,0)的距离等于M到直线x=-2的距离,由抛物线的定义求出曲线C的方程;
(II)设直线l的方程为x=my+2,代入抛物线方程,利用韦达定理,即可得出结论.
(II)设直线l的方程为x=my+2,代入抛物线方程,利用韦达定理,即可得出结论.
解答:解:(Ⅰ)依题意知,动点M到定点F(2,0)的距离等于M到直线x=-2的距离,
曲线C是以原点为顶点,F(2,0)为焦点的抛物线.
∴曲线C的方程是y2=8x.
(II)设直线l的方程为x=my+2,代入抛物线方程,可得:y2-8my-16=0
设A(x1,y1),B(x2,y2),则y1+y2=8m,y1y2=-16,
∴△AOB的面积=
|OF||y1-y2|=
≥8,即△AOB的面积最小值为8.
曲线C是以原点为顶点,F(2,0)为焦点的抛物线.
∴曲线C的方程是y2=8x.
(II)设直线l的方程为x=my+2,代入抛物线方程,可得:y2-8my-16=0
设A(x1,y1),B(x2,y2),则y1+y2=8m,y1y2=-16,
∴△AOB的面积=
| 1 |
| 2 |
| 64m2+64 |
点评:本题主要考查了轨迹方程,考查直线与圆锥曲线的综合问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
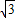 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.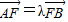 .当2≤λ≤3时,求直线l斜率k的取值范围•
.当2≤λ≤3时,求直线l斜率k的取值范围•