Question

圆台的上、下底面半径分别为6和12，平行于底面的截面自上而下分母线为2：1两部分，则截面的面积为

100π

．

Answer 1

分析：如图，圆台的轴截面为ABCD，截得此圆台的圆锥的轴截面为OAB，圆台上底半径为FC=6，下底半径为EB=12，截面半径为MN．利用三角形相似求得OC、MN的值，即可求得截面的面积．

解答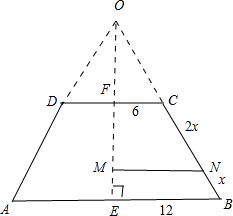：解：如图，圆台的轴截面为ABCD，截得此圆台的圆锥的轴截面为OAB，
圆台上底半径为FC=6，下底半径为EB=12，截面半径为MN，
则由题意可得，可令CN=2x，BN=x．
由直角三角形OFC与直角三角形OEB相似可得

FC

EB

=

OC

OB

，即

6

12

=

OC

OC+2x+x

，
∴OC=3x．
再由△PMN与△OEB相似可得

MN

EB

=

ON

OB

，即

MN

12

=

3x+2x

3x+2x+x

，解得 MN=10，
故截面的面积为 π MN²=100π，
故答案为 100π．

点评：本题主要考查三角形相似的性质，求旋转体的截面面积，体现了数形结合的数学思想，属于中档题．