题目内容
（普通高中做）
已知等差数列
中，
为的前
项和，
．
（Ⅰ）求的通项
与；
（Ⅱ）当为何值时，为最大？最大值为多少？
（示范性高中做）
已知数列
的首项
前项和为，且
（Ⅰ）求数列的通项公式；
（Ⅱ）令
，求数列
的前n项和
．
【答案】
（示范性高中做）
解：（I）由已知
可得
两式相减得
即
从而
当
时
所以
又
所以
从而
故总有
，
又
从而
；…………6分
（II）由（I）知
因为
=
=
-
=
……………12分
练习册系列答案
阅读快车系列答案
相关题目
中，
为
项和，
.
与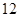
分）已知抛物线的顶点在坐标原点，焦点在
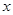轴正半轴，抛物线上一点
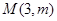到焦点的距离为
,求
的值及抛物线方程.
, 
与
的夹角为
，
(
)
当m为何值时，
与
垂直?
的体积．
(示范性高中做)求多面体
的体积．
的倾斜角的大小为
;
，过点M (5,6)的直线l与圆C交于P、Q两点，若
,
，则直线l的斜率为
;