题目内容
定义域[﹣1,1]的奇函数f(x)满足f(x)=f(x﹣2),且当x∈(0,1)时,f(x)=2x+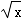 .
.
(1)求f(x)在[﹣1,1]上的解析式;
(2)求函数f(x)的值域.
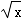 .
. (1)求f(x)在[﹣1,1]上的解析式;
(2)求函数f(x)的值域.
解:(1)当x∈(﹣1,0)时,﹣x∈(0,1),
则f(﹣x)=﹣2x+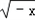
∵f(x)为[﹣1,1]的奇函数,
∴f(﹣x)=﹣f(x)
∴f(x)=2x﹣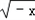
又∵f(0)=﹣f(0),
∴f(0)=0
∵f(﹣1)=﹣f(1),f(﹣1)=f(1﹣2)=f(1)
∴f(﹣1)=0,f(1)=0
∴f(x)=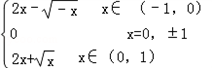
(2)∵x∈(0,1)时,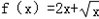 .
.
∴f'(x)=2+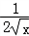 >0
>0
∴f(x)在(0,1)上为增函数,f(x)∈(0,3)
∵f(x)为[﹣1,1]的奇函数,
∴f(x)在(﹣1,1)上为增函数
∴当x∈(﹣1,1)时,f(x)∈(﹣3,3),f(±1)=0
∴函数f(x)的值域为(﹣3,3)

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
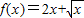 .
.  .
.