题目内容
已知函数f(x)=lnx,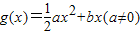
(1)当a=-2时,函数h(x)=f(x)-g(x)在其定义域内是增函数,求实数b的取值范围;
(2)令V(x)=2f(x)-x2-kx(k∈R),如果V(x)的图象与x轴交于A(x1,0)、B(x2,0)两点(0<x1<x2),且线段AB的中点为C(x,0),函数V(x)的导函数为V′(x),求证:V′(x)≠0.
【答案】分析:(1)求导函数,可得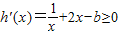 对任意x∈(0,+∞)恒成立,分离参数,求出函数的最值,即可求实数b的取值范围;
对任意x∈(0,+∞)恒成立,分离参数,求出函数的最值,即可求实数b的取值范围;
(2)利用反证法,求导函数,利用V(x)的图象与x轴交于A(x1,0)、B(x2,0)两点(0<x1<x2),且线段AB的中点为C(x,0),从而可引出矛盾.
解答:(1)解:由题意,h(x)=lnx+x2-bx,
∵函数h(x)=f(x)-g(x)在其定义域内是增函数,
∴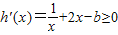 对任意x∈(0,+∞)恒成立
对任意x∈(0,+∞)恒成立
分离参数可得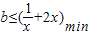 ,
,
所以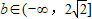 …(4分)
…(4分)
(2)证明:V(x)=2f(x)-x2-kx(k∈R),所以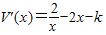
令V′(x)=0,则由题意可得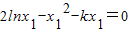 ①;
①;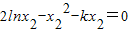 ②
②
x1+x2=2x③;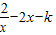 =0④
=0④
由①②得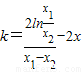
由④得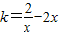
所以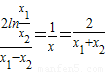 ,即
,即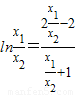 ⑤(8分)
⑤(8分)
令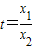 ,则
,则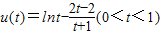 ,所以
,所以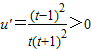
因此u(t)在(0,1)上是增函数,
所以u(t)<u(1)=0,即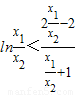 与⑤矛盾
与⑤矛盾
因此假设不成立
故V'(x)≠0(12分)
点评:本题考查导数知识的运用,考查函数的单调性,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.
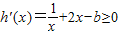 对任意x∈(0,+∞)恒成立,分离参数,求出函数的最值,即可求实数b的取值范围;
对任意x∈(0,+∞)恒成立,分离参数,求出函数的最值,即可求实数b的取值范围;(2)利用反证法,求导函数,利用V(x)的图象与x轴交于A(x1,0)、B(x2,0)两点(0<x1<x2),且线段AB的中点为C(x,0),从而可引出矛盾.
解答:(1)解:由题意,h(x)=lnx+x2-bx,
∵函数h(x)=f(x)-g(x)在其定义域内是增函数,
∴
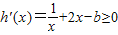 对任意x∈(0,+∞)恒成立
对任意x∈(0,+∞)恒成立分离参数可得
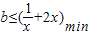 ,
,所以
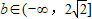 …(4分)
…(4分)(2)证明:V(x)=2f(x)-x2-kx(k∈R),所以
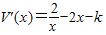
令V′(x)=0,则由题意可得
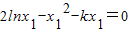 ①;
①;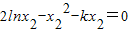 ②
②x1+x2=2x③;
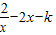 =0④
=0④由①②得
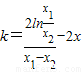
由④得
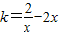
所以
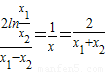 ,即
,即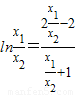 ⑤(8分)
⑤(8分)令
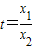 ,则
,则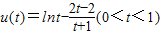 ,所以
,所以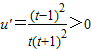
因此u(t)在(0,1)上是增函数,
所以u(t)<u(1)=0,即
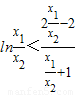 与⑤矛盾
与⑤矛盾 因此假设不成立
故V'(x)≠0(12分)
点评:本题考查导数知识的运用,考查函数的单调性,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目