题目内容
在
中，
， 满足条件的（ ）
| A．有一解 | B．有两解 | C．无解 | D．不能确定 |
C
解析试题分析：因为根据三角形中正弦定理可知：
>1，因此无解，故选C
考点：本试题主要考查了解三角形的运用。
点评：解决该试题的关键是分析已知中的两边和其中一边的对角，那么利用正弦定理得到求解，注意分析解的个数。
练习册系列答案
全优点练单元计划系列答案
相关题目
△ABC的三个内角
所对的边分别为
，
，则
A． | B． | C． | D． |
在
中，已知
，那么这个三角形一定是（ ）
| A．等边三角形 | B．直角三角形 |
| C．等腰三角形 | D．等腰直角三角形 |
在△ABC中，角A,B,C所对的边分别为
，若
，则
的值为( )
A． | B． | C． | D． |
B．
C．
D．
在一座20m高的观测台顶测得对面一水塔仰角为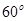
，塔底俯角为
，那么这座塔的高为( )
A． m | B． m |
C． m | D． m |
在△ABC中，若
，则其面积等于（ ）
A． | B． | C． | D． |
已知△
的三边长成公差为
的等差数列，且最大角的正弦值为
，则这个三角形的周长是（ ）
A． | B． | C． | D． |
在
中，
，则
的解的个数是 （ ）
| A．2个 | B．1个 | C．0个 | D．不确定的 |