题目内容
对于函数
（0＜x＜π），下列结论正确的是
- A.有最大值而无最小值
- B.有最小值而无最大值
- C.有最大值且有最小值
- D.既无最大值又无最小值
D
分析：首先利用二倍角公式整理化简，得到结果为正弦的倒数与1的和，根据所给的自变量的区间，得到正弦函数的值域，根据基本初等函数求出值域．
解答：=
=
∵0＜x＜π，由原式得到x≠
∵sinx∈（0，1）
∴
∴f（x）∈（2，+∞）
∴函数没有最小值没有最大值，
故选D．
点评：本题考查三角函数的化简求值，本题解题的关键是对函数式进行整理，得到最简形式，再根据基本初等函数的性质来求值域，本题是一个中档题目．
分析：首先利用二倍角公式整理化简，得到结果为正弦的倒数与1的和，根据所给的自变量的区间，得到正弦函数的值域，根据基本初等函数求出值域．
解答：
==∵0＜x＜π，由原式得到x≠
∵sinx∈（0，1）
∴
∴f（x）∈（2，+∞）
∴函数没有最小值没有最大值，
故选D．
点评：本题考查三角函数的化简求值，本题解题的关键是对函数式进行整理，得到最简形式，再根据基本初等函数的性质来求值域，本题是一个中档题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（0＜x＜π），下列结论正确的是（ ）
（0＜x＜π），下列结论正确的是（ ）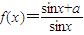
（0＜x＜π），下列结论正确的是（ ）
（0＜x＜π），下列结论正确的是（ ）
（0＜x＜π），下列结论正确的是（ ）