题目内容
(本小题满分16分)
已知函数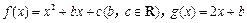 ,且对于任意
,且对于任意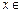 R,恒有
R,恒有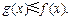
(1)证明: ;
;
(2)设函数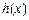 满足:
满足: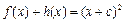 ,证明:函数
,证明:函数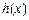 在
在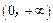 内没有零点.
内没有零点.
已知函数
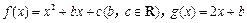 ,且对于任意
,且对于任意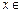 R,恒有
R,恒有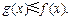
(1)证明:
 ;
;(2)设函数
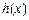 满足:
满足: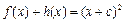 ,证明:函数
,证明:函数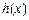 在
在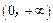 内没有零点.
内没有零点.略
(1)任意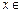 R,恒有
R,恒有 ,即
,即 恒成立,
恒成立,
所以 ,化简得
,化简得 . 于是
. 于是 . ………………………4分
. ………………………4分
而 ,所以
,所以 ,故
,故 .………………………8分
.………………………8分
(2) . ………………………10分
. ………………………10分
由(1)知 ,
, . ………………………13分
. ………………………13分
于是当 时,
时, ,
,
故函数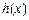 在
在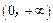 内没有零点. ………………………16分
内没有零点. ………………………16分
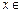 R,恒有
R,恒有 ,即
,即 恒成立,
恒成立,所以
 ,化简得
,化简得 . 于是
. 于是 . ………………………4分
. ………………………4分而
 ,所以
,所以 ,故
,故 .………………………8分
.………………………8分(2)
 . ………………………10分
. ………………………10分由(1)知
 ,
, . ………………………13分
. ………………………13分于是当
 时,
时, ,
,故函数
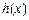 在
在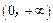 内没有零点. ………………………16分
内没有零点. ………………………16分
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从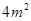 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )
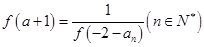 ,则a2011的值为
,则a2011的值为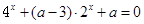 在
在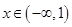 上有两个不等实根,则实数a的取值范围是 ( )
上有两个不等实根,则实数a的取值范围是 ( )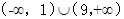
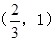
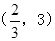
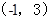
 ,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元?
,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元? 是一次函数,且
是一次函数,且 ,
, ,求
,求 ,求
,求 的解是
的解是