题目内容
双曲线x2-y2=1的顶点到其渐近线的距离等于（ ）A．
B．
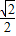
C．1
D．
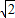
【答案】分析：求出双曲线的渐近线方程，顶点坐标，利用点到直线的距离求解即可．
解答：解：双曲线x2-y2=1的顶点坐标（1，0），其渐近线方程为y=±x，
所以所求的距离为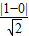
=
．
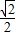故选B．
点评：本题考查双曲线的简单性质的应用，考查计算能力．
解答：解：双曲线x2-y2=1的顶点坐标（1，0），其渐近线方程为y=±x，
所以所求的距离为
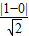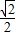=．故选B．
点评：本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
若椭圆
+
=1过抛物线y2=8x的焦点，且与双曲线x2-y2=1有相同的焦点，则该椭圆的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|