题目内容
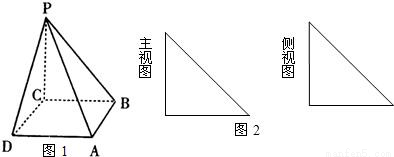
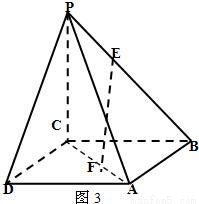
如下图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.求证:PA∥平面EDB.

证明:如图,建立空间直角坐标系D—xyz,连结AC交BD于G,连结EG.

依题意,设正方形ABCD的边长为a,则得A(a,0,0),P(0,0,a),E(0,a2,a2),
因为底面是正方形,
所以G是正方形的中心.
所以G(![]() ,
,![]() ,0).
,0).
所以![]() =(a,0,-a),
=(a,0,-a),![]() =(
=(![]() ,0,-
,0,-![]() ).
).
所以![]() =2
=2![]() .
.
因为E![]() PA,所以PA∥EG.
PA,所以PA∥EG.
而EG![]() 平面EDB,且PA
平面EDB,且PA![]() 平面EDB,
平面EDB,
所以PA∥平面EDB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
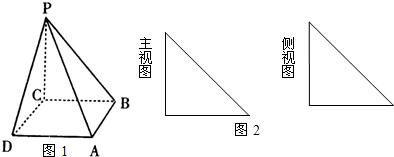
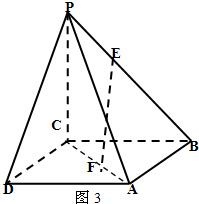
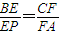 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
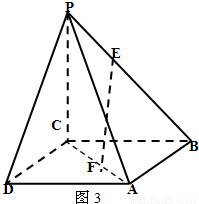
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.

 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
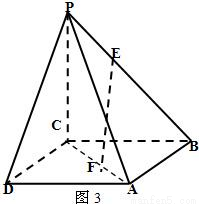
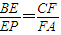 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.